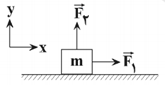
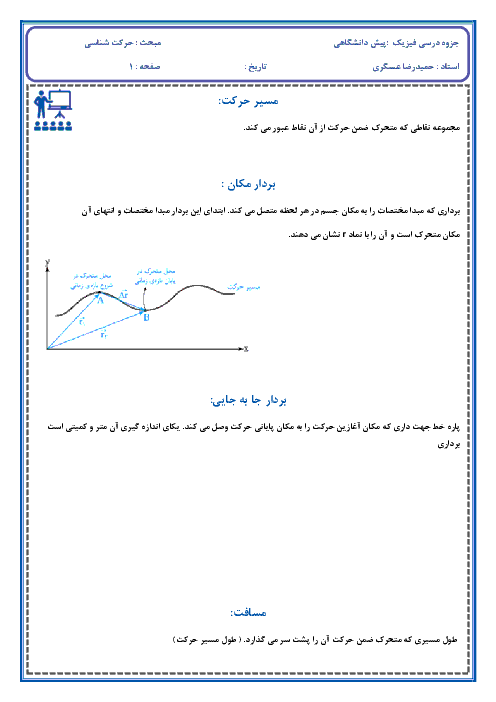
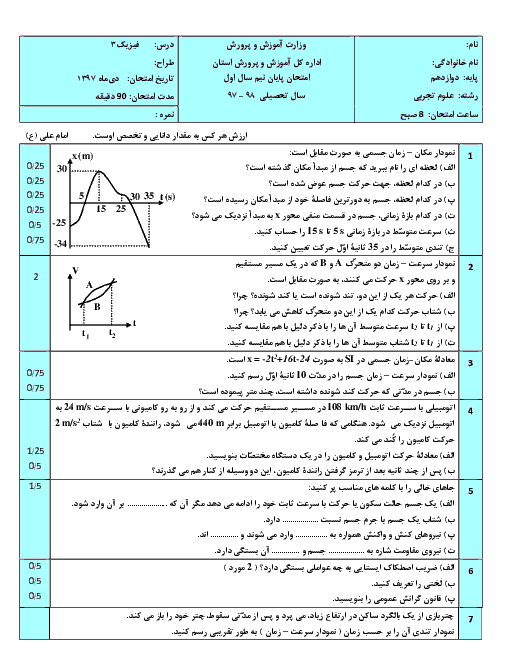
ابتدا معادلهٔ نيروی عمودی سطح را به‌دست می‌آوريم، داريم:

${{({{\overrightarrow{F}}_{net}})}_{y}}=0\Rightarrow {{\overrightarrow{F}}_{N}}+{{\overrightarrow{F}}_{2}}+\overrightarrow{W}=0$

$\Rightarrow {{\overrightarrow{F}}_{N}}=-\overrightarrow{W}-{{\overrightarrow{F}}_{2}}\xrightarrow[\overrightarrow{W}=-mg\overrightarrow{j}]{{{\overrightarrow{F}}_{2}}=(8-t)\overrightarrow{j}}{{\overrightarrow{F}}_{N}}=mg\overrightarrow{j}-(8-t)\overrightarrow{j}\xrightarrow{mg=18N}{{\overrightarrow{F}}_{N}}=(10+t)\overrightarrow{j}$

اكنون لحظه‌ای كه جسم در آستانهٔ حركت قرار می‌گيرد را به‌دست می‌آوريم:

${{F}_{1}}={{f}_{s,\max }}$

$\xrightarrow[{{F}_{N}}=10+t,{{\mu }_{s}}=0/5]{{{f}_{s,\max }}={{\mu }_{s}}{{F}_{N}},{{F}_{1}}=3t}3t=0/5(10+t)$

$t=\frac{5}{2/5}=2s$

پس از لحظهٔ $t=2s$، اصطكاک بين جسم و سطح از نوع جنبشی خواهد شد و در اين حالت نيروی خالص وارد بر جسم برابر است با:

${{F}_{net}}={{F}_{1}}-{{\mu }_{K}}{{F}_{N}}=3t-0/4(10+t)\Rightarrow {{F}_{net}}=2/6t-4$

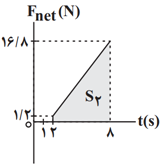
اكنون نمودار نيروی خالص برحسب زمان را برای اين جسم می‌كشيم. دقت شود تا لحظهٔ $t=2s$، چون جسم در حال سكون است، بنابراين نيروی خالص وارد بر آن برابر صفر است. با توجه به اين‌كه سطح محصور بين نمودار نيروی خالص و زمان برابر با تغيير تكانه است، داريم:

${{(\Delta p)}_{2s-8s}}={{S}_{2}}=\frac{(1/2+16/8)\times 6}{2}=54\frac{kg.m}{s}$

$\xrightarrow[{{p}_{t=8s}}=mv,m=1/8kg]{{{p}_{t=2s}}=0}1/8v=54\Rightarrow v=30\frac{m}{s}$