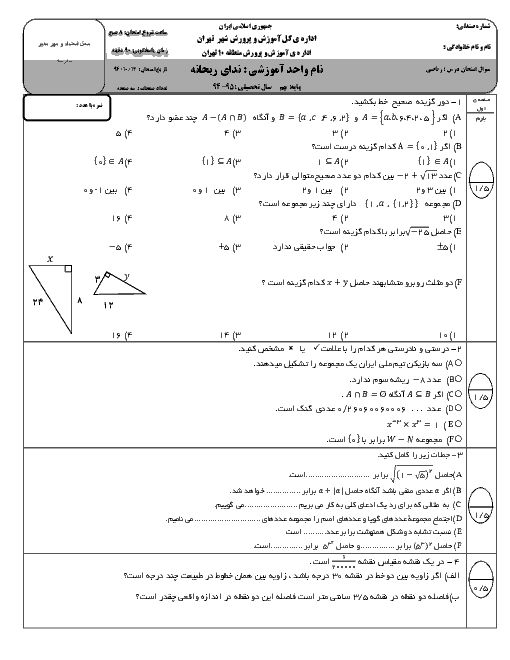
به ازای چه مقداری از m، معادلهی خطی که از نقاط $ \begin{bmatrix} 1 \\ 1 \end{bmatrix} $ و $ \begin{bmatrix} m^2 \\ m \end{bmatrix} $ میگذرد با خطی به معادلهی $ y-mx=x+m $ موازی است؟
1 )
$ m=0 , m=-1 $
2 )
$ m=-1 , m=-2 $
$ m=0 , m=-2 $
4 )
$ m=-1 , m=1 $
پاسخ تشریحی :
تحلیل ویدئویی تست
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...