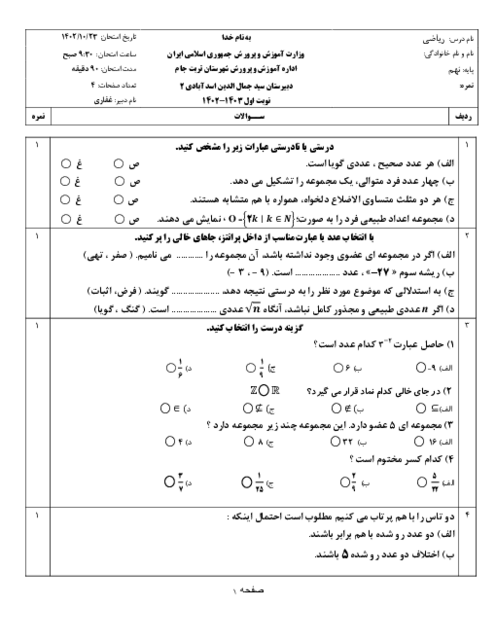
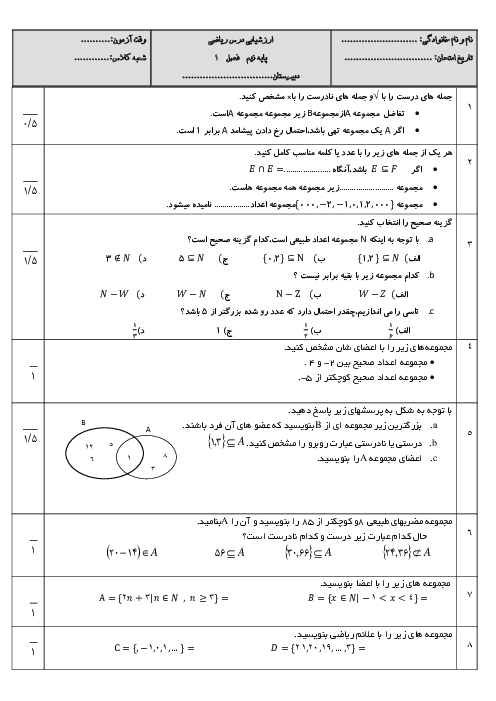
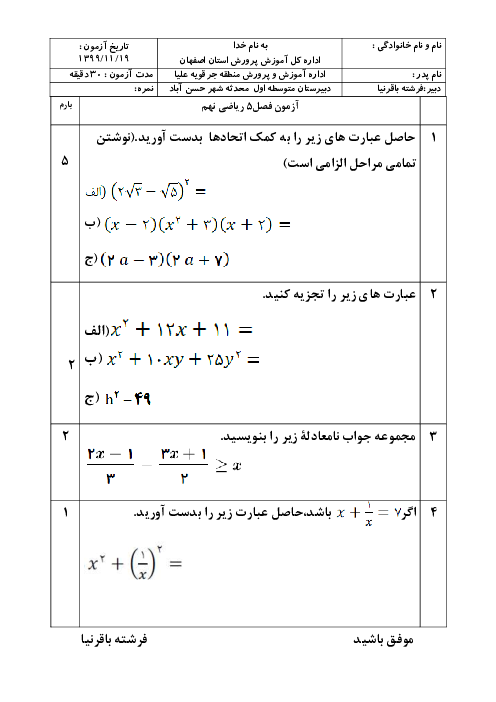حاصل عبارت ${{\mathop x\nolimits^2 + 1} \over {\mathop x\nolimits^2 - 4x - 21}} - {{x - 3} \over {x + 3}}$ کدام است؟
1 )
${{10(x - 2)} \over {(x + 3)(x + 7)}}$
2 )
${{10(x + 2)} \over {(x + 7)(x - 3)}}$
${{10(x - 2)} \over {(x - 7)(x + 3)}}$
4 )
${{(x - 3)} \over {(x + 3)(x + 7)}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
زهرا شیخ الاسلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...