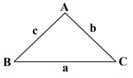
نكته (قضيۀ سينوس‌ها): در هر مثلث دلخواه نسبت اندازهٔ هر ضلع به سينوس زاويۀ مقابل آن برابر با قطر دايرهٔ محيطی مثلث است. 

$\frac{a}{\operatorname{Sin}\hat{A}}=\frac{b}{\operatorname{Sin}\hat{B}}=\frac{c}{\operatorname{Sin}\hat{C}}=2R$         (شعاع دایرهٔ محیطی است$R$)

نكته (قضيۀ فيثاغورس): مثلث $ABC$ در رأس $A$ قائم‌الزاويه است، اگر و تنها اگر: ${{a}^{2}}={{b}^{2}}+{{c}^{2}}$ با استفاده از قضيۀ سينوس‌ها داريم:

$\frac{a}{\operatorname{Sin}\hat{A}}=2R\Rightarrow \operatorname{Sin}\hat{A}=\frac{a}{2R}$

$\frac{b}{\operatorname{Sin}\hat{B}}=2R\Rightarrow \operatorname{Sin}\hat{B}=\frac{b}{2R}$

$\frac{c}{\operatorname{Sin}\hat{C}}=2R\Rightarrow \operatorname{Sin}\hat{C}=\frac{c}{2R}$

با جایگذاری این مقدار در عبارت ${{\operatorname{Sin}}^{2}}\hat{A}={{\operatorname{Sin}}^{2}}\hat{B}+{{\operatorname{Sin}}^{2}}\hat{C}$ داریم:

${{(\frac{a}{2R})}^{2}}={{(\frac{b}{2R})}^{2}}+{{(\frac{c}{2R})}^{2}}\Rightarrow \frac{{{a}^{2}}}{4{{R}^{2}}}=\frac{{{b}^{2}}+{{c}^{2}}}{4{{R}^{2}}}\Rightarrow {{a}^{2}}={{b}^{2}}+{{c}^{2}}$

بنابراين مثلث $ABC$ در رأس $A$ قائم‌الزاويه است؛ يعنی: $\hat{A}={{90}^{{}^\circ }}$