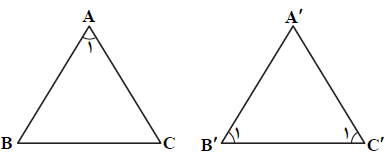
در مثلث متساویالساقين $ABC$ زاويهی رأس برابر يك راديان و در مثلث متساویالساقين ${A}'{B}'{C}'$ زاويهی مجاور به قاعده برابر يك راديان است. اگر طول ساقهای دو مثلث برابر باشد، مساحت مثلث ${A}'{B}'{C}'$ چند برابر مساحت مثلث $ABC$ است؟
1 )
$\operatorname{Sin}1$
2 )
$2\operatorname{Sin}1$
3 )
$\operatorname{Cos}1$
$2\operatorname{Cos}1$
پاسخ تشریحی :