سری دوم: آزمون آزمایشی کنکور سراسری رشته علوم تجربی | مادهٔ درسی ریاضیات (ریاضی 1 و 2 و 3)
متوسطه دوم نظری
کنکور سراسری
علوم تجربی
ریاضی
اردیبهشت
شامل مباحث:
ریاضیات پایه
معادله درجه دوم، گویا و رادیکالی
تابع
مثلثات
توابع نمایی و لگاریتمی
حد، پیوستگی و مجانب
مشتق و کاربردهای آن
الگو و دنباله
آمار
احتمال
ترسیمهای هندسی، هندسه تجسمی و مقاطع مخروطی
استدلال، تالس و تشابه
هندسه تحلیلی
شمارش، جایگشت و ترکیب
ریاضیات پایه
معادله درجه دوم، گویا و رادیکالی
تابع
مثلثات
توابع نمایی و لگاریتمی
حد، پیوستگی و مجانب
مشتق و کاربردهای آن
الگو و دنباله
آمار
احتمال
ترسیمهای هندسی، هندسه تجسمی و مقاطع مخروطی
استدلال، تالس و تشابه
هندسه تحلیلی
شمارش، جایگشت و ترکیب
تعداد سوالات: 30
سطح دشواری:
متوسط
شروع:
آزاد
پایان:
آزاد
مدت پاسخگویی:
60 دقیقه
رایگان
5,000 تومان
لطفا برای اطمینان از عملکرد و تجربه بهتر از مرورگرهای مدرن و به روز مانند کروم یا فایرفاکس استفاده کنید.

پیش نمایش صفحه اول فایل
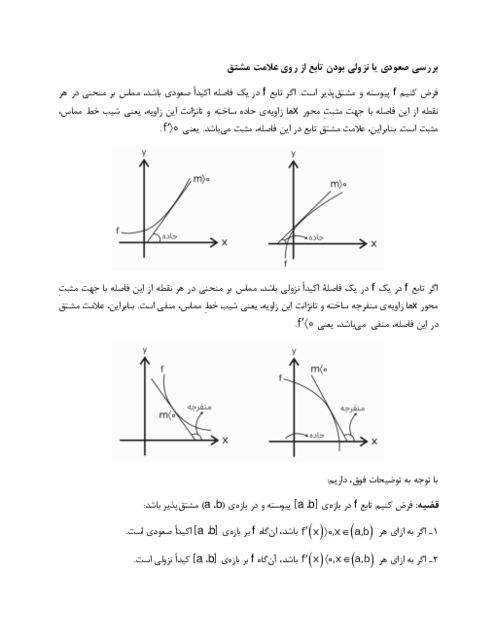
اگر $f(x)=x^2-5x$، مشتق تابع $f(cosx)$ در x=0 چند است؟