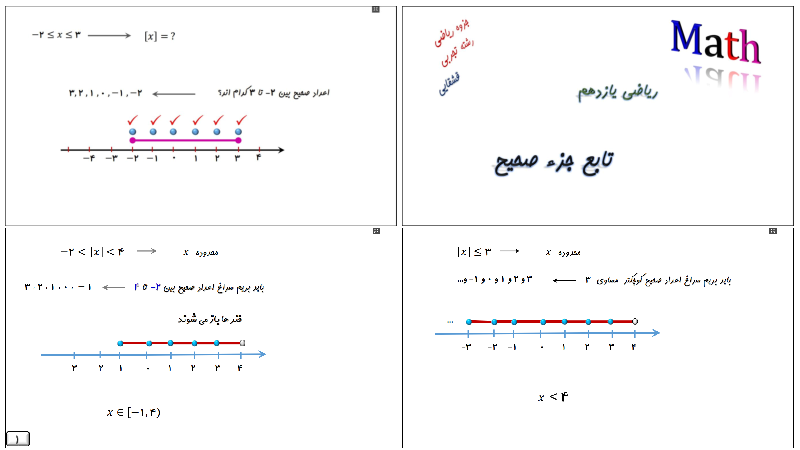
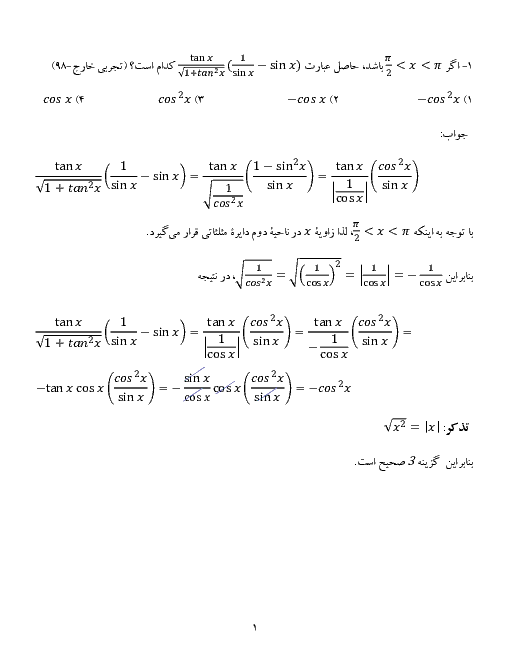
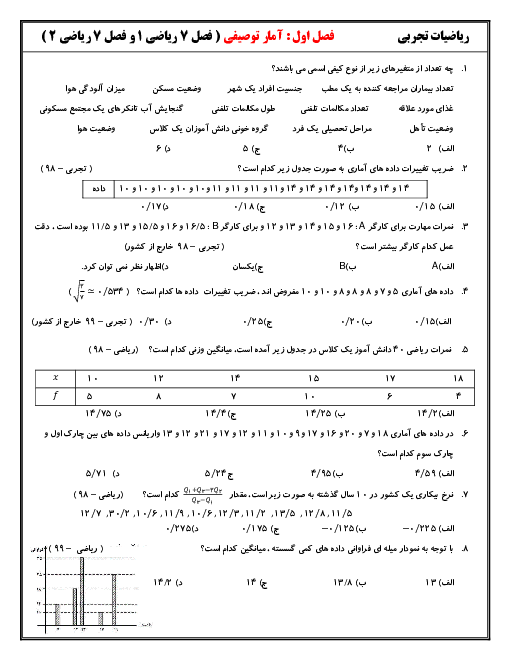
ابتدا $x$ را برحسب $y$ پیدا میکنیم:
$y=-\sqrt{\frac{x+7}{2}}-3\Rightarrow \sqrt{\frac{x+7}{2}}=-y-3$
توجه كنيد در عبارت بهدست آمده بايد $-y-3$ مقداری نامنفی باشد. (زيرا جواب يك راديكال همواره نامنفی است.)
حال میتوان دو طرف تساوی را به توان $2$ رساند: $-y-3\ge 0\Rightarrow y\le -3$
$\sqrt{\frac{x+7}{2}}=-y-3\Rightarrow \frac{x+7}{2}={{(-y-3)}^{2}}\Rightarrow x+7=2({{y}^{2}}+6y+9)\Rightarrow x=2{{y}^{2}}+12y+11$
جای $x$ و $y$ را عوض كرده تا ضابطهی ${{f}^{-1}}(x)$ بهدست آيد:
${{f}^{-1}}(x)=2{{x}^{2}}+12x+11\,\,;\,\,x\le -3$