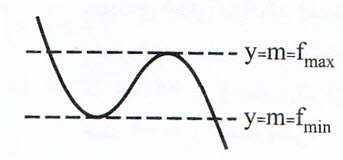با توجه به نمودار تابع ، به ازای کدام مقادیر خط به معادلهٔ با نمودار تابع مفروض فقط در دو نقطه مشترک است؟

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

ریاضی پنجم فصل اول ریاضی ششم فصل اول الگوی مثلثی عدد شش رقمی بدون تکرار تغییر فیزیکی و شیمیایی ریاضی چهارم خط به خط زیست دهم جمله خبری نهاد چیست چه اعدادی بر ۶ بخش پذیرند مسند چیست مراحل روش علمی درس اول زبان هشتم با معنی و تلفظ

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

درس 3: رسم نمودار تابع حسابان (2) دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

با توجه به نمودار تابع $f(x)=-\frac{2}{3}{{x}^{3}}+{{x}^{2}}+12x$، به ازای کدام مقادیر $m$ خط به معادلهٔ $y=m$ با نمودار تابع مفروض فقط در دو نقطه مشترک است؟

1 )

$27$ یا $-\frac{44}{3}$

2 )

$24$ یا $-\frac{44}{3}$

3 )

$24$ یا $-\frac{16}{3}$

4 )

$27$ یا $-\frac{16}{3}$

نمایش پاسخ

با توجه به نمودار تابع درجه‌ٔ سوم مقابل، $m$ باید برابر با ماکزیمم یا می‌نیمم نسبی تابع باشد، تا خط $y=m$ نمودار تابع $f$ را در دو نقطه قطع کند، بنابراین:

$f(x)=-\frac{2}{3}{{x}^{3}}+{{x}^{2}}+12x$

$f'(x)=-2{{x}^{2}}+2x+12=0\Rightarrow {{x}^{2}}-x-6=0$

$\Rightarrow (x-3)(x+2)=0$

$\Rightarrow \left\{ \begin{align} & f(3)=-\frac{2}{3}({{3}^{3}})+{{3}^{3}}+12\times 3=27 \\ & f(-2)=-\frac{2}{3}{{(-2)}^{3}}+{{(-2)}^{2}}+12\times (-2)=\frac{-44}{3} \\ \end{align} \right.$

$\Rightarrow m=27\,\,\,ya\,\,\,\frac{-44}{3}$