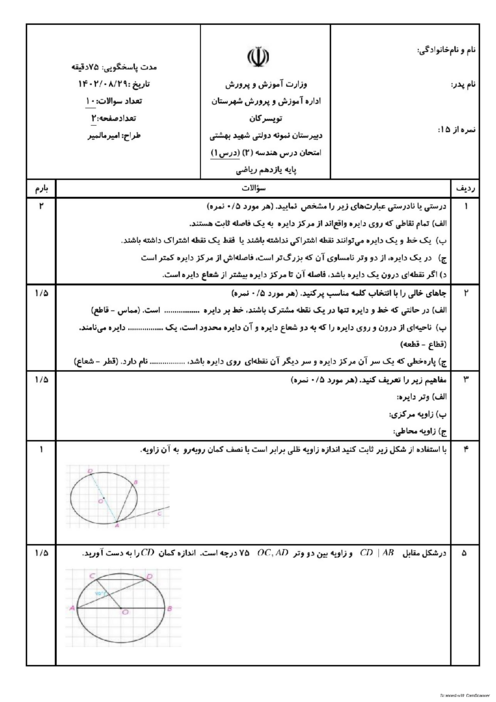
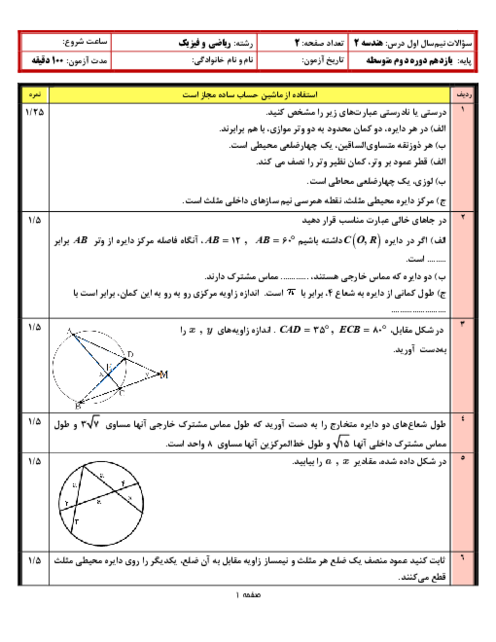
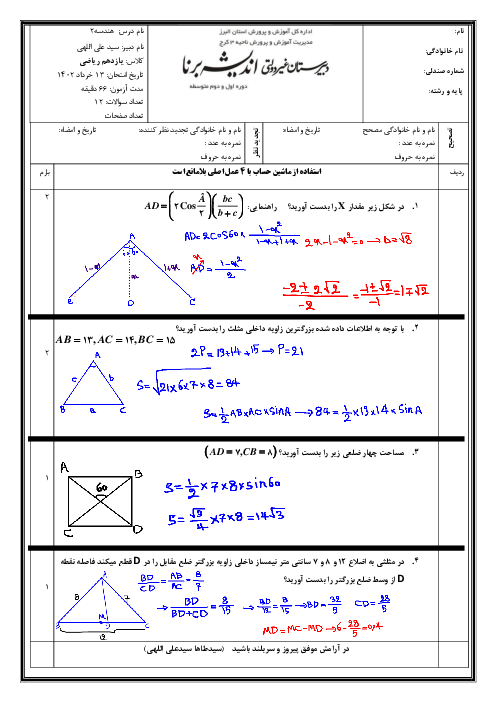
درس 1: مفاهیم اولیه و زاویه‌ها در دایره
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
مساحت قطاعی از دایرۀ $C(O,R)$ که زاویۀ محاطی روبه‌رو به کمان آن قطاع برابر ${{72}^{{}^\circ }}$ باشد، چقدر است؟$(\pi =3,R=10)$
تحلیل ویدئویی تست
محسن ذوالفقاری 
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...