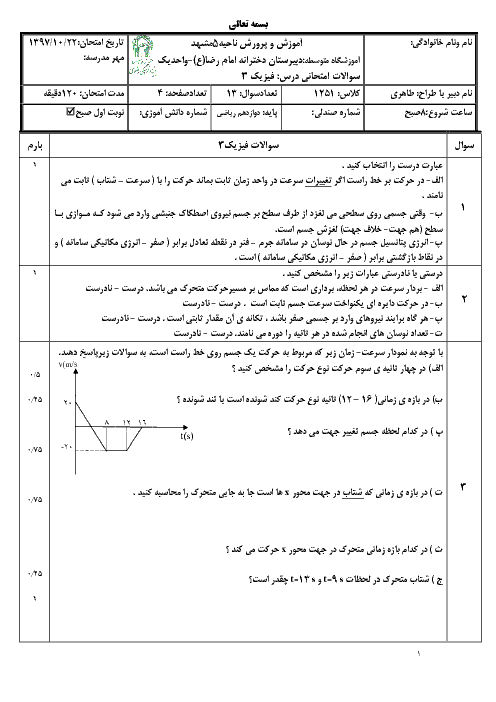
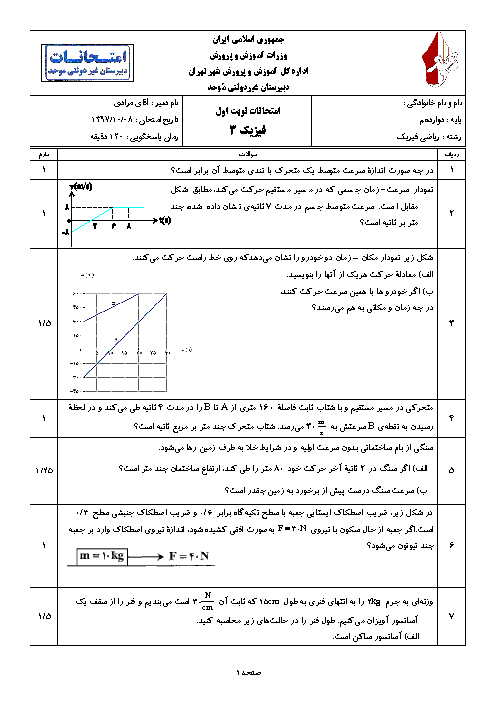
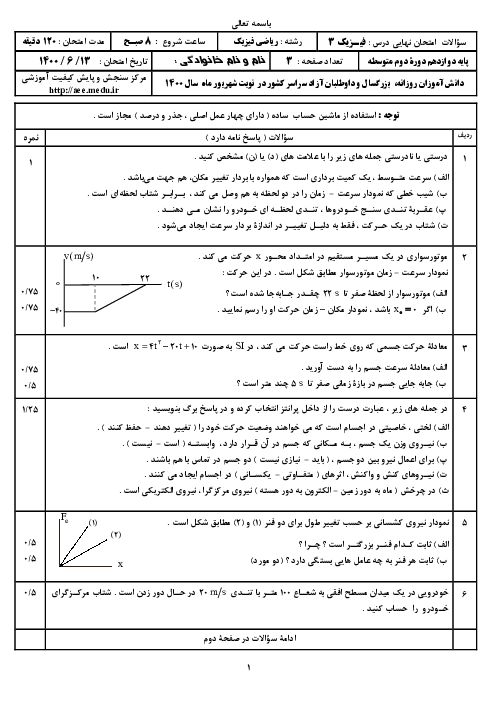
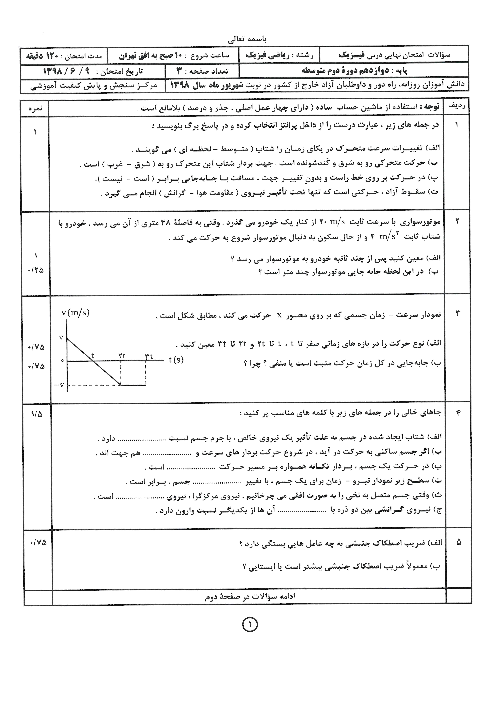
اگر تندی موج $S$ را ${{v}_{S}}$ و تندی موج $P$ را ${{v}_{P}}$ بنامیم، داریم:

${{v}_{S}}=\frac{40}{100}{{v}_{P}}=\frac{2}{5}{{v}_{P}}$

برای موج اولیهٔ $P$ می‌توان نوشت:

$\Delta {{x}_{P}}={{v}_{P}}\Delta {{t}_{P}}$

و برای موج اولیهٔ $S$ می‌توان نوشت:

$\Delta {{x}_{S}}={{v}_{S}}\Delta {{t}_{S}}$

$\Rightarrow \left\{ \begin{matrix} \Delta {{t}_{P}}=\frac{\Delta x}{{{v}_{P}}}  \\ \Delta {{t}_{S}}=\frac{\Delta x}{{{v}_{S}}}  \\ \end{matrix} \right.\xrightarrow{\Delta {{t}_{S}}-\Delta {{t}_{P}}=1/5\min }\frac{\Delta x }{{{v}_{S}}}-\frac{\Delta x}{{{v}_{P}}}=1/5\times 60$

$\Rightarrow \Delta x\left( \frac{1}{{{v}_{S}}}-\frac{1}{{{v}_{P}}} \right)=1/5\times 60$

$\xrightarrow{{{v}_{S}}=0/4{{v}_{P}}}\Delta x\left( \frac{1}{0/4{{v}_{P}}}-\frac{1}{{{v}_{P}}} \right)=1/5\times 60$

$\xrightarrow{\Delta x=300km}\frac{300\times 1/5}{{{v}_{P}}}=1/5\times 60$

${{v}_{P}}=5\frac{km}{s}\Rightarrow {{v}_{S}}=\frac{2}{5}{{v}_{P}}=2\frac{km}{s}$

$\Delta x={{v}_{S}}\Delta {{t}_{S}}\Rightarrow 300=2\times \Delta {{t}_{S}}\Rightarrow \Delta {{t}_{S}}=150s=\frac{5}{2}\min $