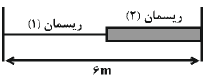
با استفاده از رابطهٔ تندی امواج عرضی در ريسمان كشيده، داريم:

$v=\sqrt{\frac{F}{\mu }}\Rightarrow \frac{{{v}_{2}}}{{{v}_{1}}}=\sqrt{\frac{{{\mu }_{1}}}{{{\mu }_{2}}}}\Rightarrow \frac{{{v}_{2}}}{{{v}_{1}}}=\sqrt{\frac{1}{4}}\Rightarrow \frac{{{v}_{2}}}{{{v}_{1}}}=\frac{1}{2}$

از طرفی امواج عرضی با تندی ثابت در طول هر ريسمان منتشر می‌شوند، بنابراين داريم:

$\begin{align}
  & v=\frac{L}{t}\Rightarrow \frac{{{v}_{2}}}{{{v}_{1}}}=\frac{{{L}_{2}}}{{{L}_{1}}}\times \frac{\Delta {{t}_{1}}}{\Delta {{t}_{2}}} \\
 & \xrightarrow{\Delta {{t}_{1}}=\Delta {{t}_{2}}}\frac{1}{2}=\frac{{{L}_{2}}}{{{L}_{1}}}\Rightarrow {{L}_{2}}=\frac{1}{2}{{L}_{1}}\,\,\,\,\,\,(*) \\
\end{align}$

از طرفی داریم:

${{L}_{1}}+{{L}_{2}}=6\xrightarrow{(*)}{{L}_{1}}+\frac{1}{2}{{L}_{1}}=6\Rightarrow {{L}_{1}}=4m$