شکل زیر، تصویری از موجی عرضی در یک ریسمان کشیده را در لحظهٔ نشان می‌دهد. اگر سرعت انتشار موج باشد در بازهٔ زمانی تا حرکت ذرهٔ چگونه است؟

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

نوسان و امواج و برهم کنش‌های موج فیزیک کنکور سراسری دوره دوم متوسطه- نظری علوم تجربی

شکل زیر، تصویری از موجی عرضی در یک ریسمان کشیده را در لحظهٔ $t=0$ نشان می‌دهد. اگر سرعت انتشار موج $2\frac{m}{s}$ باشد در بازهٔ زمانی ${{t}_{1}}=0/25s$ تا ${{t}_{2}}=0/35s$ حرکت ذرهٔ $M$ چگونه است؟

1 )

ابتدا کند شونده و سپس تند شونده

2 )

ابتدا تند شونده و سپس کند شونده

3 )

پیوسته کند شونده

4 )

پیوسته تند شونده

نمایش پاسخ

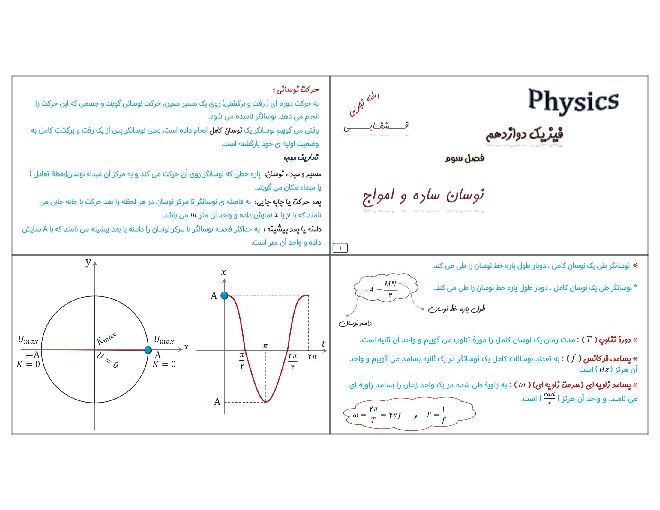
گام اول: با توجه به تصویر داده شده از موج $\frac{\lambda }{2}=20$ و در نتیجه $\lambda =40cm$ است. بنابراین برای محاسبهٔ دورهٔ تناوب داریم:

$\lambda =vT\Rightarrow 0/4=2\times T\Rightarrow T=0/2s$

گام دوم: حالا ${{t}_{1}}$ و ${{t}_{2}}$ را برحسب دورهٔ تناوب می‌نویسیم:

${{t}_{1}}=0/25s\xrightarrow{T=0/2s}{{t}_{1}}=\frac{5}{4}T=T+\frac{T}{4}$

${{t}_{2}}=0/35s\xrightarrow{T=0/2s}{{t}_{2}}=\frac{7}{4}T=T+\frac{3T}{4}$

گام سوم: ذرٔه $M$ در لحظهٔ $t=0$ در مکان $y=-A$ قرار دارد.
بنابراین موقعیت این ذره در لحظه‌های ${{t}_{1}}$ و ${{t}_{2}}$ به شکل زیر است.
با توجه به شکل در بازهٔ زمانی ${{t}_{1}}$ تا ${{t}_{2}}$، نوسانگر ابتدا در حال دور شدن از مبدأ و سپس در حال نزدیک‌ شدن به مبدأ است. بنابراین در این بازهٔ زمانی، حرکت متحرک ابتدا کند شونده و سپس تند شونده است.