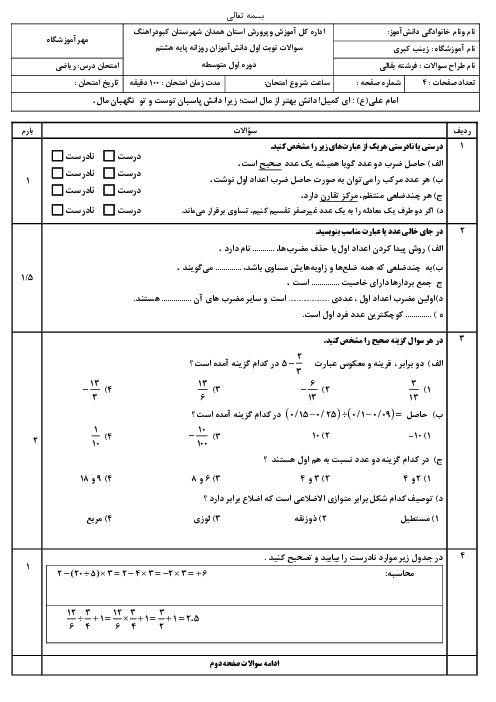
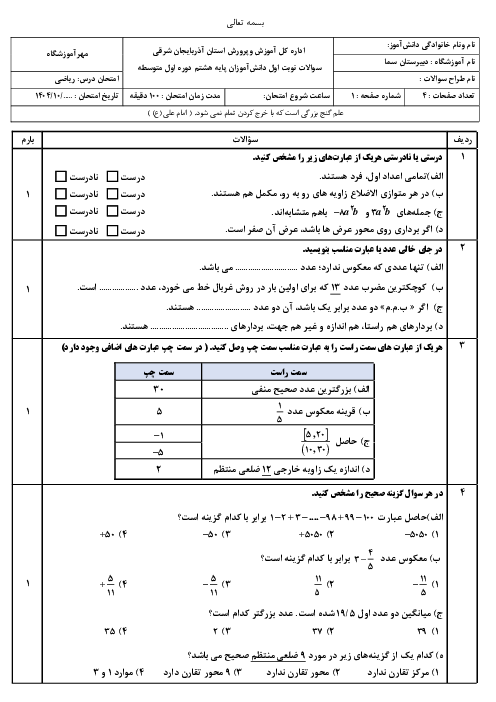
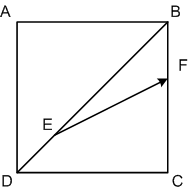
در مربع $ABCD$ نقطه‌ی $E$ را روی قطر $BD$ و نقطه‌ی $F$ را روی ضلع $BC$ طوری اختیار می کنیم که $CF=2FB,BF=2ED$. در این صورت $\vec{EF}$ بر حسب $\vec{AB}$ و $\vec{AD}$ برابر است با:
$\frac{2}{3} \vec{AB} - \frac{1}{3} \vec{AD}$
2 )
$\frac{2}{3} \vec{AB} - \frac{2}{3} \vec{AD}$
3 )
$\frac{1}{3} \vec{AB} - \frac{1}{3} \vec{AD}$
4 )
$ \vec{AB} - \frac{1}{3} \vec{AD}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...