درس 1: مفاهیم اولیه و زاویهها در دایره
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
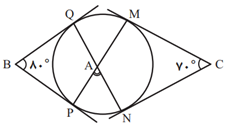
در شكل زير، اضلاع زاويههای $B$ و $C$ بر دايره مماساند. اندازهٔ زاويهٔ $P\hat{A}N$ کدام است؟
1 )
${{45}^{{}^\circ }}$
2 )
${{60}^{{}^\circ }}$
${{75}^{{}^\circ }}$
4 )
${{90}^{{}^\circ }}$