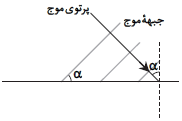
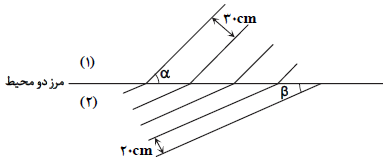
شكل زير، وضعيت جبهۀ موج تخت را در عبور موج از محيط $(1)$ به محيط $(2)$ نشان می‌دهد. اگر $\alpha$ زاويۀ ميان جبهه‌های موج در محيط $(1)$ و مرز دو محيط و $\beta $ زاويۀ ميان جبهه‌های موج در محيط $(2)$ و مرز دو محيط باشد، كدام‌یک از موارد زير درست است؟
1 )
$\sin \alpha =\frac{2}{3}\sin \beta $
2 )
$\cos \alpha =\frac{2}{3}\cos \beta $
$\sin \alpha =\frac{3}{2}\sin \beta $
4 )
$\cos \alpha =\frac{3}{2}\cos \beta $
پاسخ تشریحی :
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...