پودمان 3: معادله‌های درجۀ دوم
ریاضی1 فنی
دهم
متوسطه دوم فنی
مشترک شاخۀ فنی و حرفه‌ای
درسنامه آموزشی این مبحث
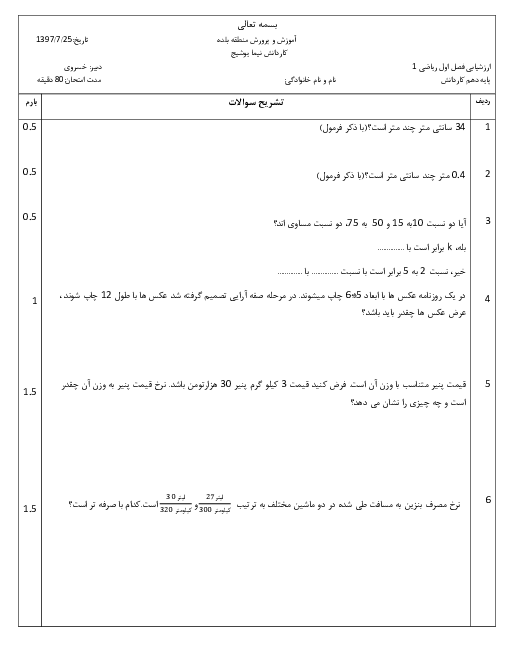
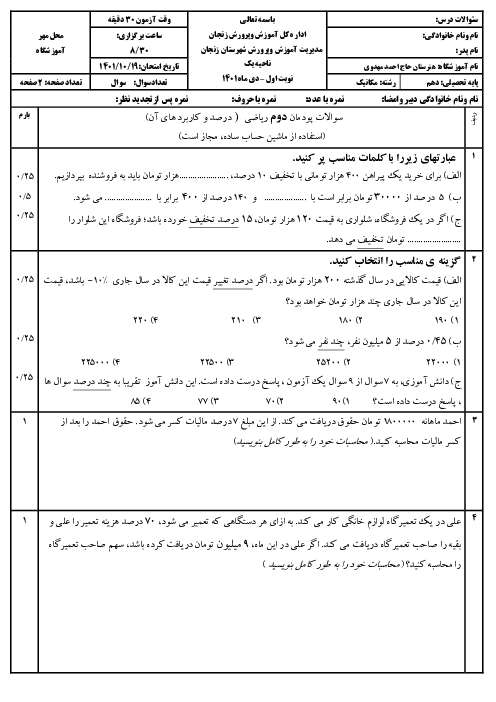
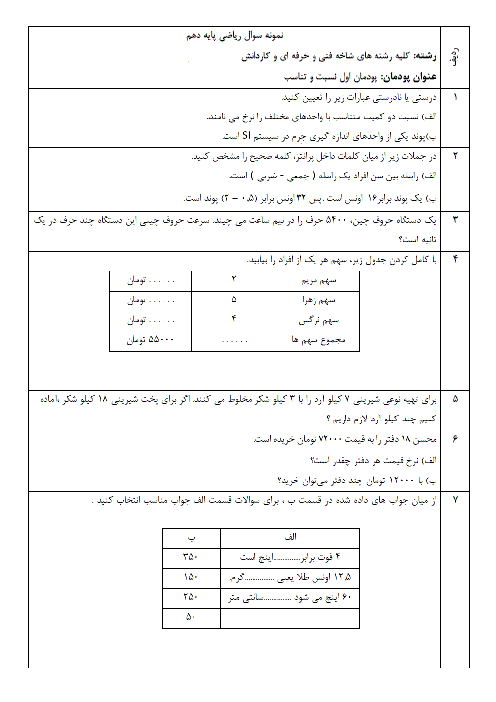
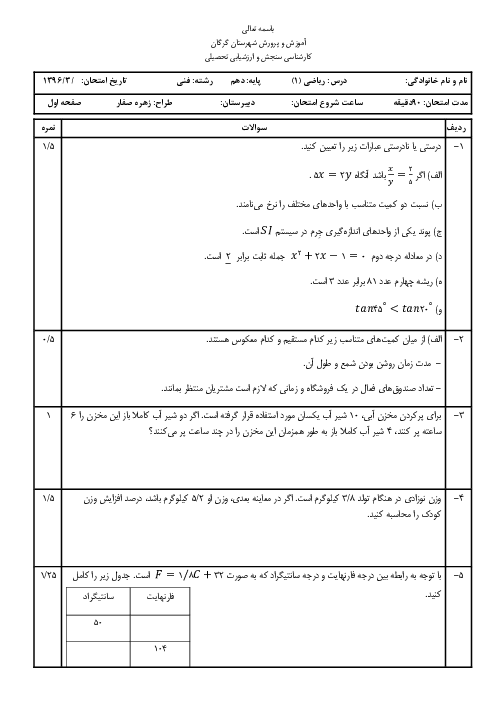
برای حل معادله‌ی درجه دوم $(5x + 1)(x - 1) = 3$ به روش هندسی، محل برخورد کدام دو نمودار را می‌توان به دست آورد؟
1 )
${y_2} = x + 1,{y_1} = 2{x^2}$
2 )
${y_2} = - \frac{4}{5}x + \frac{4}{5},{y_1} = {x^2}$
${y_2} = \frac{4}{5}x + \frac{4}{5},{y_1} = {x^2}$
4 )
${y_2} = x - 1,{y_1} = 2{x^2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...