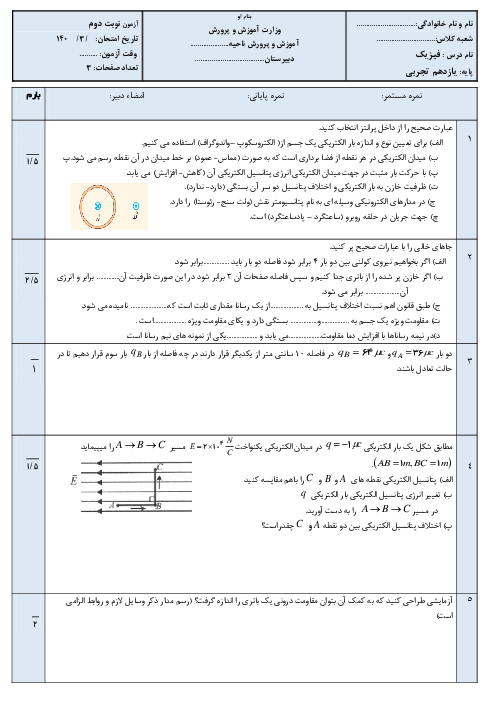
درحرکت از A تا B، با استفاده از روابط زیر داریم:

$\left\{ \begin{matrix}   \Delta U=q\Delta V  \\   \Delta U=-{{W}_{E\,}}  \\   \Delta U=-\Delta K  \\\end{matrix} \right.\Rightarrow \left\{ \begin{matrix}   -q\Delta V={{W}_{E}}  \\   \Delta K={{W}_{E}}\,\,\,\,\,\,  \\\end{matrix} \right.\Rightarrow \left\{ \begin{matrix}   5\times {{10}^{-6}}\times ({{V}_{B}}-1000)=5\times {{10}^{-3}}  \\   \frac{1}{2}\times 2\times {{10}^{-3}}v_{B}^{2}=5\times {{10}^{-3}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,  \\\end{matrix}\Rightarrow \left\{ \begin{matrix}   {{V}_{B}}=2000V  \\   {{v}_{B}}=\sqrt{5}m/s  \\\end{matrix} \right. \right.$

درحرکت از B تا C با استفاده از روابط زیر داریم:

$\left\{ \begin{matrix}   \Delta U=q\Delta V  \\   \Delta U=-\Delta K  \\\end{matrix}\Rightarrow \Delta K=-q\Delta V\Rightarrow \frac{1}{2}\times 2\times {{10}^{-3}} \right.\times {{(\sqrt{5})}^{2}}=5\times {{10}^{-6}}\times (3000-2000)\Rightarrow {{v}_{C}}=\sqrt{10}m/s\,\,,\,\,\frac{{{v}_{C}}}{{{v}_{B}}}=\frac{\sqrt{10}}{\sqrt{5}}=\sqrt{2}$