نمودار سرعت - زمان دو متحرک و که در مبدأ زمان روی مسیری از یک نقطه عبور می‌کنند، مطابق شکل زیر است. اگر و باشد، به ترتیب از راست به چپ، چند ثانیه پس از شروع حرکت… | فیزیک (3) ریاضی دوازدهم شماره 68947

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

قسمت 3: حرکت با شتاب ثابت فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

نمودار سرعت - زمان دو متحرک $A$ و $B$ که در مبدأ زمان روی مسیری از یک نقطه عبور می‌کنند، مطابق شکل زیر است. اگر ${{a}_{A}}=3\frac{m}{{{S}^{2}}}$ و ${{a}_{B}}=1/5\frac{m}{{{S}^{2}}}$ باشد، به ترتیب از راست به چپ، چند ثانیه پس از شروع حرکت سرعت دو متحرک برابر می‌شود و چند ثانیه پس از شروع حرکت دو متحرک به هم می‌رسند؟

1 )

$15 ، 7/5$

2 )

$10 ، 5$

3 )

$15 ، 5$

4 )

$10 ، 7/5$

نمایش پاسخ

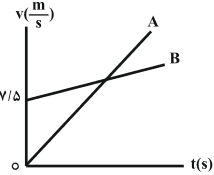
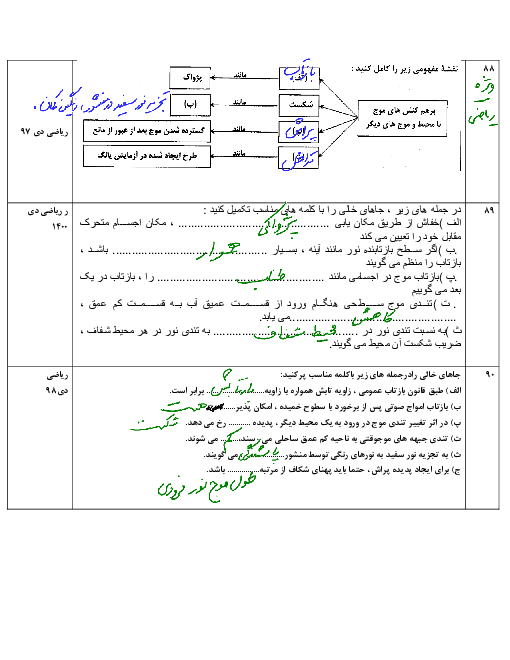
چون نمودار سرعت - زمان هر دو متحرک به صورت خط راستی با شیب غیرصفر است، بنابراین شتاب حرکت متحرک‌های $A$ و $B$ ثابت است و بنابراین معادلهٔ سرعت - زمان آن‌ها به صورت زیر است.

${{v}_{A}}={{a}_{A}}t+{{v}_{{{0}_{A}}}}=3t+0\Rightarrow {{v}_{A}}=3t$

${{v}_{B}}={{a}_{B}}t+{{v}_{{{0}_{B}}}}=1/5t+7/5\Rightarrow {{v}_{B}}=1/5t+7/5$

در لحظه‌ای که سرعت دو متحرک برابر می‌شود، داریم:

${{v}_{A}}={{v}_{B}}\Rightarrow 3t'=1/5'+7/5\Rightarrow t'=5s$

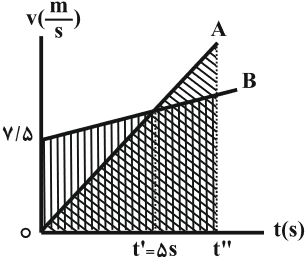
برای به دست آوردن لحظه‌ای که دو متحرک به هم می‌رسند، چون مساحت زیر نمودار سرعت - زمان برابر با جابه‌جایی متحرک است و این دو متحرک بدون تغییر جهت حرکت می‌کنند، داریم:

$\Delta {{x}_{A}}=\Delta {{x}_{B}}\Rightarrow \frac{t''\times 3t''}{2}=\frac{7/5+(1/5t''+7/5)}{2}t''\Rightarrow t''=10s$

به عنوان تمرین، با استفاده از معادلهٔ مکان - زمان دو متحرک $A$ و $B$، لحظه‌ای که دو متحرک به هم می‌رسند را محاسبه کنید.