درس 1: آشنایی با منطق ریاضی
آمار و احتمال
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
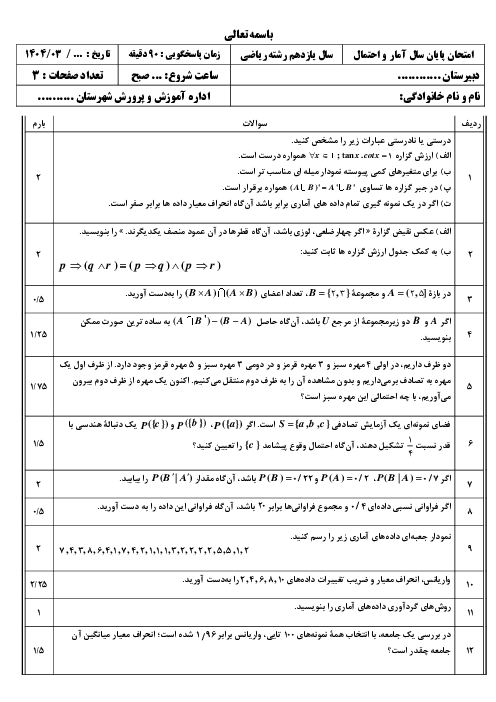
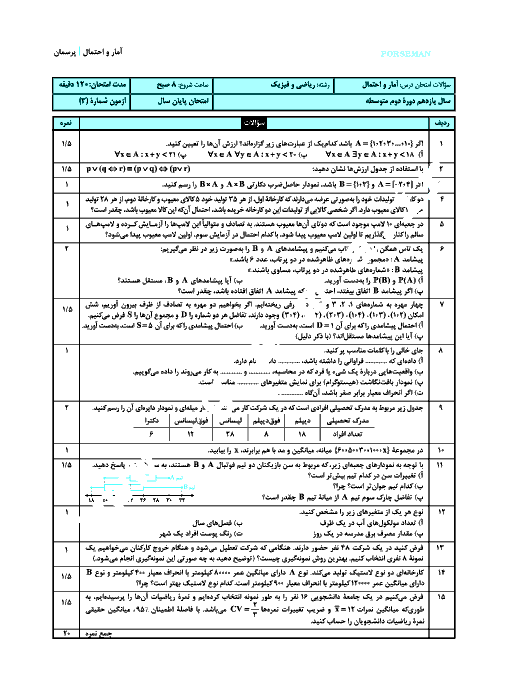
کدام گزینه، گزارهٔ «$\forall x\in P-\left\{ 2,3 \right\};\exists k\in N;(x=6k+1)\vee (x=6k-1)$» را بیان می‌کند؟ (P مجموعهٔ اعداد اول و k عددی طبیعی است.)
هر عدد اول بزرگ‌تر از 3 به صورت 6k+1 یا 6k-1 است.
2 )
اگر عددی به صورت 6k+1 یا 6k-1 باشد عددی اول غیر از 2 و 3 است.
3 )
مقداری مانند k در مجموعهٔ اعداد طبیعی وجود دارد، طوری که 6k+1 یا 6k-1، عدد اول و بزرگ‌تر از 3 باشد.
4 )
اگر عددی عضو مجموعهٔ اعداد اول غیر از 2 و 3 باشد، آنگاه قطعاً 6 برابرش به علاوه یا منهای یک، عدد اول است.
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...