در شکل زیر نمودار شتاب ـ زمان متحرکی به جرم که روی محور در حرکت است، نشان داده شده است. اگر سرعت اولیهٔ متحرک باشد، اندازهٔ تکانهٔ آن در لحظهٔ چند است؟ | فیزیک (3) ریاضی دوازدهم شماره 74189

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

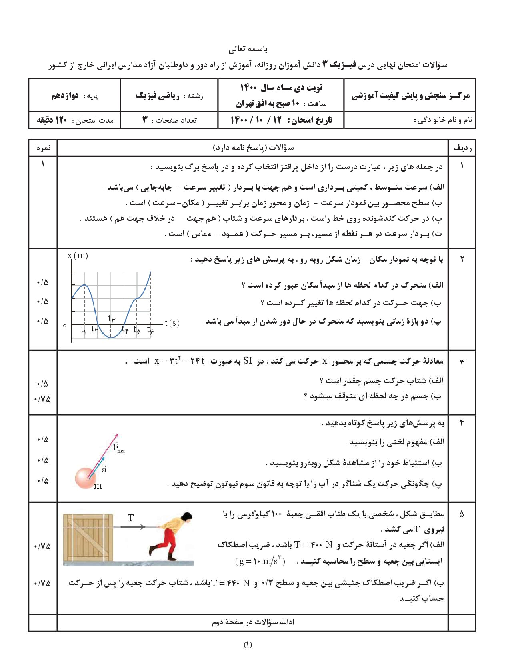
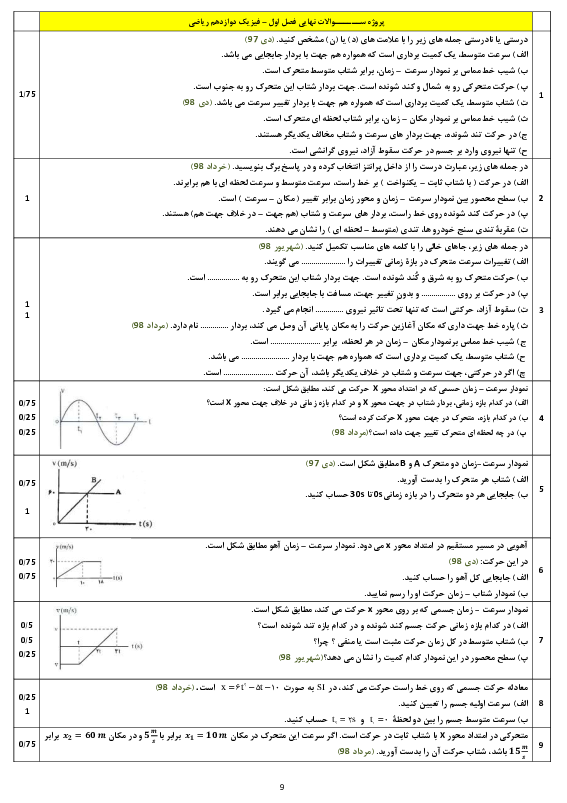
قسمت 3: تکانه و قانون دوم نیوتون فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

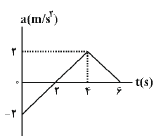
در شکل زیر نمودار شتاب ـ زمان متحرکی به جرم $2kg$ که روی محور $x$ در حرکت است، نشان داده شده است. اگر سرعت اولیهٔ متحرک $4m/s$ باشد، اندازهٔ تکانهٔ آن در لحظهٔ $t=6s$ چند $\frac{kg.m}{s}$ است؟

1 )

$4$

2 )

$8$

3 )

$12$

4 )

$20$

نمایش پاسخ

بنا به رابطهٔ $P=mv$ برای محاسبهٔ اندازهٔ تکانه در لحظهٔ $t=6s$ باید سرعت در اين لحظه را به دست آوريم. چون شتاب حركت ثابت نيست، كافيست مساحت سطح محصور بين نمودار شتاب – زمان و محور زمان كه برابر با تغییرات سرعت است را محاسبه کرده و سپس از رابطهٔ $\Delta v=v-{{v}_{\circ }}$ سرعت را حساب کنیم.

$\begin{align}
& \Delta v={{S}_{1}}+{{S}_{2}}=\frac{-2\times 2}{2}+\frac{(6-2)\times 2}{2}\Rightarrow \Delta v=-2+4=2\frac{m}{s} \\
& \Delta v=v-{{v}_{\circ }}\xrightarrow[\Delta v=2\frac{m}{s}]{{{v}_{\circ }}=4\frac{m}{s}}2=v-4\Rightarrow v=6\frac{m}{s} \\
\end{align}$

حال اندازهٔ تكانه را حساب می‌کنيم.

$p=mv\xrightarrow[v=6\frac{m}{s}]{m=2kg}p=2\times 6=12\frac{kg.m}{s}$