درس 1: آشنایی با منطق ریاضی
آمار و احتمال
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
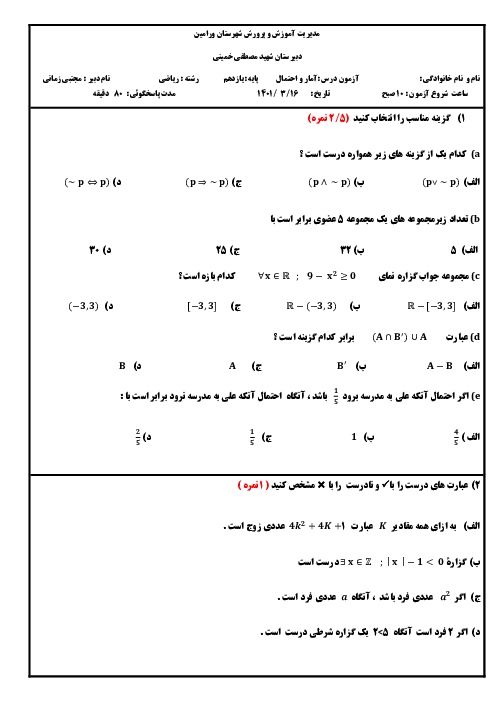
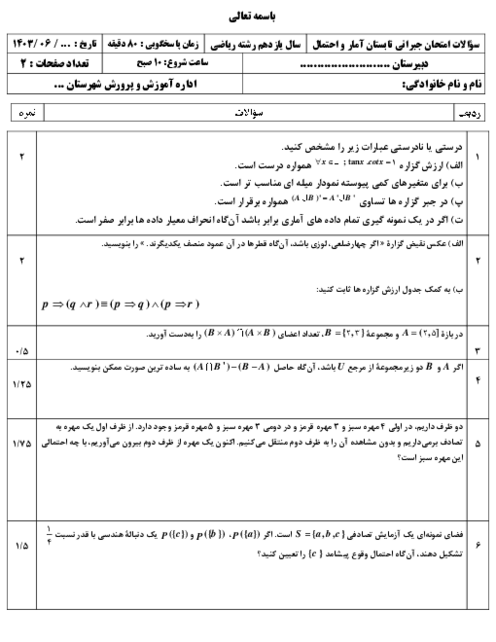
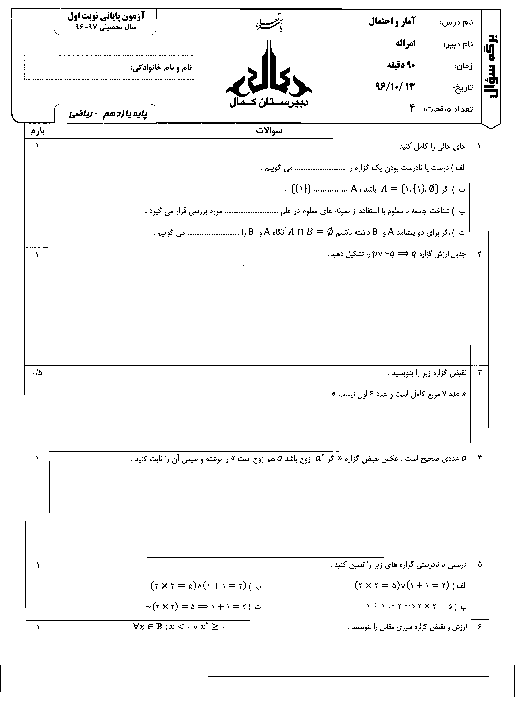
نقیض گزارۀ $\forall x\in (-\infty ,0);x-\frac{1}{x}\le -2$، کدام است و ارزش نقیض چیست؟
1 )
نادرست و $\exists x\in (-\infty ,0);x-\frac{1}{x}\gt-2$
2 )
درست و $\forall x\in (-\infty ,0);x-\frac{1}{x}\gt-2$
3 )
نادرست و $\forall x\in (-\infty ,0);x-\frac{1}{x}\gt-2$
درست و $\exists x\in (-\infty ,0);x-\frac{1}{x}\gt-2$
پاسخ تشریحی :
تحلیل ویدئویی تست
علی رحیمی 
زهرا شیخ الاسلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...