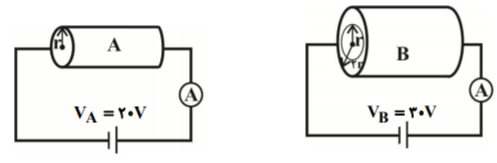
ابتدا سطح مقطع دو رسانا را به‌دست می‌آوريم:

${{A}_{A}}=\pi {{r}^{2}}$

${{A}_{B}}=\pi (r_{2}^{2}-r_{1}^{2})=\pi ({{(2r)}^{2}}-{{r}^{2}})=3\pi {{r}^{2}}$

طبق رابطهٔ $R=\rho \frac{L}{A}$ نسبت مقاومت دو رسانا را به‌دست می‌آوريم:

$R=\rho \frac{L}{A}\Rightarrow \frac{{{R}_{A}}}{{{R}_{B}}}=\frac{{{\rho }_{A}}}{{{\rho }_{B}}}\times \frac{{{L}_{A}}}{{{L}_{B}}}\times \frac{{{A}_{B}}}{{{A}_{A}}}\xrightarrow[{{L}_{B}}=1/5{{L}_{A\,,\,}}{{A}_{B}}=3\pi {{r}^{2}}]{{{\rho }_{A}}=\frac{1}{2}{{\rho }_{B}}\,,\,{{A}_{A}}=\pi {{r}^{2}}}$

$\frac{{{R}_{A}}}{{{R}_{B}}}=\frac{\frac{1}{2}{{\rho }_{B}}}{{{\rho }_{B}}}\times \frac{{{L}_{A}}}{1/5{{L}_{A}}}\times \frac{3\pi {{r}^{2}}}{\pi {{r}^{2}}}=\frac{1}{2}\times \frac{2}{3}\times 3=1$

حال طبق رابطهٔ قانون اهم می‌توان نوشت:

$I=\frac{V}{R}\Rightarrow \frac{{{I}_{A}}}{{{I}_{B}}}=\frac{{{V}_{A}}}{{{V}_{B}}}\times \frac{{{R}_{B}}}{{{R}_{A}}}=\frac{20}{30}\times 1=\frac{2}{3}$