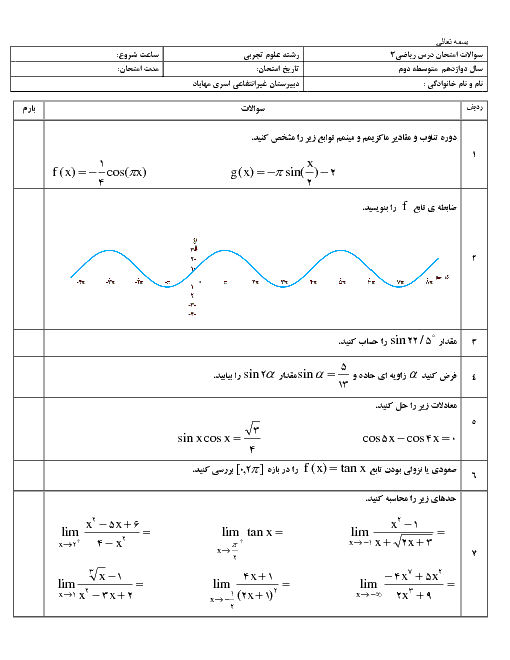
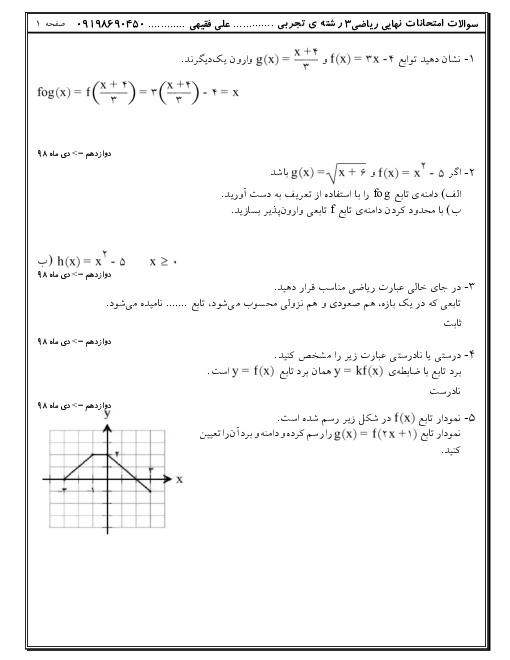
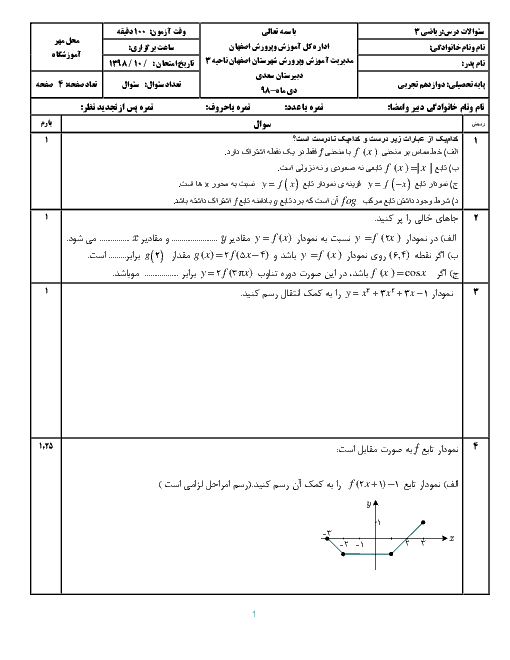
ورق فلزی مربع شکل به طول ضلع یک متر را در نظر بگیرید. میخواهیم از چهار گوشهٔ آن مربعهای کوچکی به ضلع x برش بزنیم و آنها را کنار بگذاریم. سپس لبه جعبه را به اندازه x بر میگردانیم تا یک جعبه در باز ساخته شود. مقدار x چقدر باشد تا حجم جعبه حداکثر مقدار ممکن گردد.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!