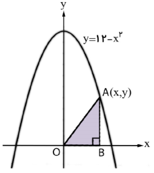
مطابق شکل زیر، نقطه A در ناحیه اول دستگاه مختصات روی منحنی $y = 12 - {x^2}$ قرار دارد.
با استفاده از جدول تغییرات، مختصات نقطه A را چنان بیابید که مساحت مثلث قائمالزاویه OAB بیشترین مقدار ممکن را داشته باشد.
پاسخ تشریحی :

گاما رو نصب کن!
جستجو
پربازدیدها: #{{ tag.title }}
به پاس اعتمادی که به گاما داشتی، ما اشتراک ویژهای رو برات فعال کردیم تا بدون هیچ نگرانی از محدودیت زمانی، از سرویسهای ویژه گاما استفاده کنی.
اگه به اطلاعات بیشتری نیاز داری راهنمای تغییرات جدید رو ببین.
از همراهیت با گاما سپاسگزاریم.
با تقدیم احترام
با سپاس! گزارش شما ثبت شد.