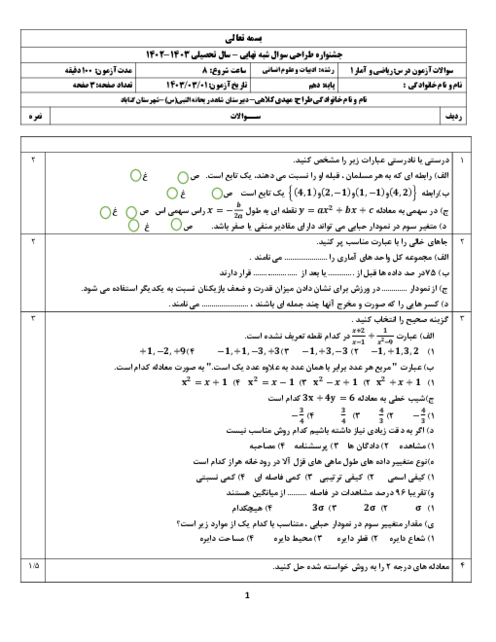
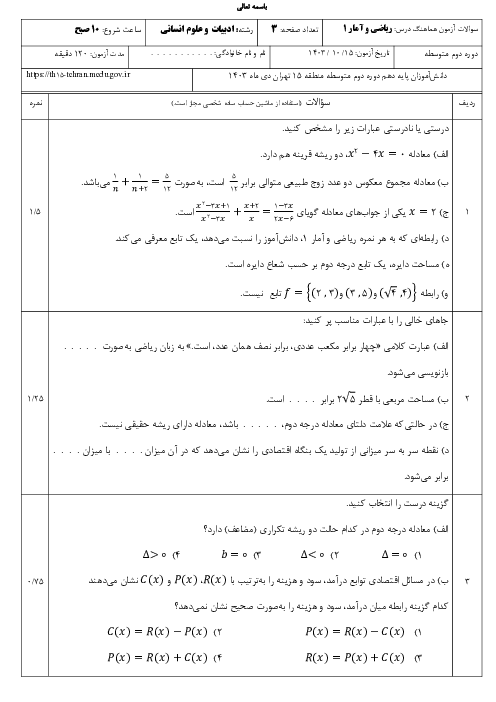
اگر طول اولیه را ${x_1}$ و عرض اولیه را ${y_1}$ در نظر بگیریم، داریم:
${y_1} = \frac{2}{3}{x_1} - 3$
عرض مستطیل 4 واحد افزایش یافته است، یعنی:
${y_2} = {y_1} + 4$
اگر ${x_1}$ به اندازهٔ $a$ واحد افزایش یافته باشد، داریم:
${x_2} = {x_1} + a$
${y_2} = \frac{2}{3}{x_2} - 3$
${y_1} + 4 = \frac{2}{3}({x_1} + a) - 3$
$ \Rightarrow {y_1} + 4 = \frac{2}{3}{x_1} + \frac{2}{3}a - 3 \to {y_1} = \frac{2}{3}{x_1} - 3 \to 4 = \frac{2}{3}a$
$ \Rightarrow a = 4 \times \frac{3}{2} \Rightarrow a = 6$
طول مستطیل 6 واحد و عرض آن 4 واحد افزایش یافته است. از آنجا که محیط مستطیل برابر با $2(x + y)$ است، محیط به اندازهٔ 20 واحد افزایش خواهد یافت.
راهحل دوم:
$y = \frac{2}{3}x - 3 \Rightarrow 3y = 2x - 9 \Rightarrow x = \frac{3}{2}y + \frac{9}{2}$
با توجه به این رابطه اگر $y$ به اندازهٔ 4 واحد تغییر کند طول $\frac{3}{2} \times 4 = 6$ واحد تغییر میکند.