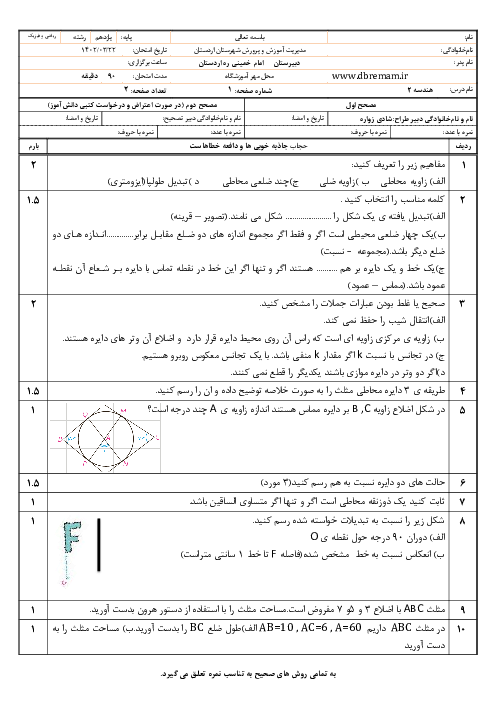
درس 3: چند ضلعی‌های محاطی و محیطی
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
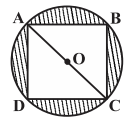
دايرهٔ محيطی مربعی به ضلع 2 را رسم كرده‌ايم . مساحت ناحيهٔ محدود بين مربع و دايرهٔ محيطی آن، چند برابر مساحت مربع است؟
$\frac{\pi }{2}-1$
2 )
$\pi -2$
3 )
$\frac{\pi -1}{2}$
4 )
$\frac{\pi -3}{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...