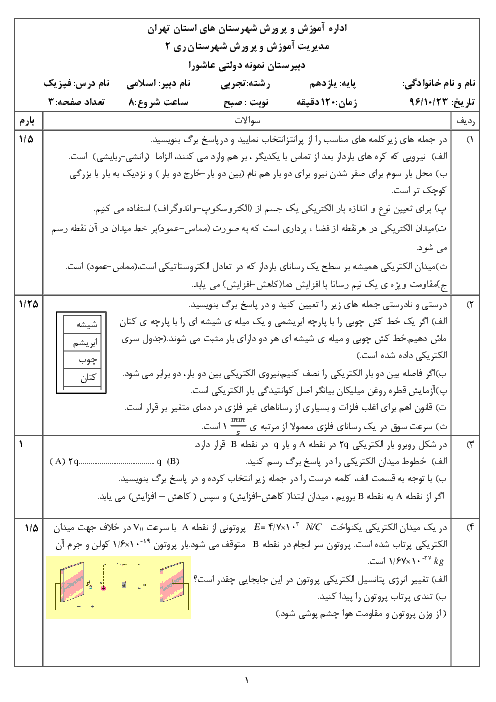
با توجه به شکل مثلث، فاصلهٔ بین بارهای ${q}'$ و $3q$ برابر $\sqrt{3a}$ میباشد. پس اگر بزرگی نیرویی که بارهای q و $3q$ بر ${q}'$ وارد میکنند بهترتیب ${{F}_{1}}$ و ${{F}_{2}}$ بنامیم، خواهیم داشت:
$F=k\frac{|{{q}_{1}}||{{q}_{2}}|}{{{r}^{2}}}\Rightarrow \left\{ \begin{matrix}
{{F}_{1}}=\frac{kq{q}'}{{{a}^{2}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\
{{F}_{2}}=\frac{k(3q)({q}')}{{{(\sqrt{3}a)}^{2}}}=\frac{kq{q}'}{{{a}^{2}}} \\
\end{matrix} \right.$
دو نیروی ${{\overrightarrow{F}}_{1}}$ و ${{\overrightarrow{F}}_{2}}$ برهم عمودند و بزرگی برابندشان (نیروی خالص وارد بر ${q}'$) برابر با $\frac{\sqrt{2}kq{q}'}{{{a}^{2}}}$ میشود.