اگر نمودار و به‌صورت روبه‌رو باشند، نمودار کدام است؟ | ریاضی و آمار (2) یازدهم شماره 105350

موبایل / ایمیل

لطفا کدی که به {{ identity }} ارسال شده است را وارد کنید.

کد فعال سازی :

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

لطفا برای حساب خود رمز عبور انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل / ایمیل

لطفا کدی که برای شما ارسال شده است را وارد کنید.

کد فعال سازی :

ارسال مجدد کد فعال سازی {{ countDown }}

منتظر دریافت پیامک شما ...

برای حساب خود رمز عبور جدید انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

ورود | ثبت نام

لطفا کمی صبر کنید ...

موبایل / ایمیل

رمزعبور

رمز عبور خود را فراموش کردید؟ بازیابی کنید.

هنوز عضو نشده اید؟ ثبت نام کنید.

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

درس 3: اعمال بر روی توابع ریاضی و آمار (2) یازدهم دوره دوم متوسطه- نظری ادبیات و علوم انسانی درسنامه آموزشی این مبحث

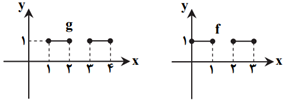
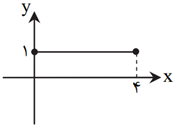
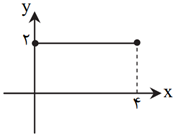
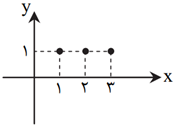
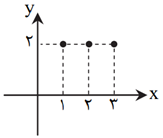
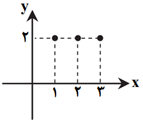
اگر نمودار $f$ و $g$ به‌صورت روبه‌رو باشند، نمودار $f+g$ کدام است؟

1 )

2 )

3 )

4 )

نمایش پاسخ

نكته: عمل جمع روی دو تابع به‌صورت زير تعريف می‌شود:

$(f+g)(x)=f(x)+g(x)$ ${{D}_{f+g}}={{D}_{f}}\bigcap {{D}_{g}}$

اول دامنۀ تابع $f+g$ كه اشتراک دامنۀ توابع $f$ و $g$ است را حساب می‌كنيم:

${{D}_{f+g}}={{D}_{f}}\bigcap{{{D}_{g}}}=\left\{ 1,2,3 \right\}$

حال بايد مقدار توابع $f$ و $g$ را در $x=1$، $x=2$ و $x=3$ با هم جمع كنيم. چون مقدار توابع $f$ و $g$ در اين نقاطبرابر است، پس اگر مقدار اين توابع را در اين سه نقطه جمع كنيم، مقدار تابع $f+g$ برابر $1+1=2$ می‌شود.بنابراين تابع $f+g$ دارای سه زوج‌مرتب با مؤلفه‌های اول ۱، 2 و ۳ و مؤلفۀ دوم ۲ است:

$f+g=\left\{ (1,2),(2,2),(3,2) \right\}$

بنابراين نمودار $f$ و $g$ به‌صورت روبه‌رو است: