راه حل اول:

نکته: علامت عبارت $y=ax+b$ برای $x$های مختلف از جدول زیر تعیین می‌شود.

که در آن $- \frac {b}{a}$ ریشه‌ی معادله‌ی $y=0$ و$a$ شیب خط است.

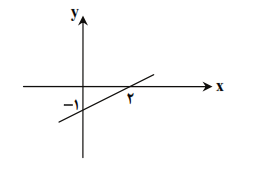
در نمودار داده شده خط محور $x$ها را در نقطه‌ای به طول ۲ قطع کرده است، پس $x=2$ ریشه‌ی معادله‌ی $y=0$ است. از طرفی چون خط با قسمت مثبت محور $x$ها زاویه‌ای کوچک‌تر از $90^{\circ}$ می‌سازد، پس شیب خط یعنی علامت $a$ مثبت است.

پس پاسخ گزینه‌ی ۴ است.

راه حل دوم:

همانطور که از نمودار مشخص است، مقادیر خط به ازای $x \gt2$ مثبت، به ازای $x \lt2$ منفی و به ازای $x=2$ صفر است. بنابارنی گزینه‌ی ۴ درست است.

نکته: به محل تقاطع هر خط با محور $y$ها عرض از مبدأ خط می‌گویند.

نکته: معادله‌ی خطی با شیب $a$ و عرض از مبدأ $b$ برابر است با: $y=ax+b$

با توجه به نمودار، خط از دو نقطه‌ی $(2,0)$ و $(0,-1)$ می‌گذرد پس شیب آن برابر $\frac {0-(-1)}{2-0}=\frac {1}{2}$ می‌باشد. از طرفی عرض از مبدأ خط برابر $-1$ است، پس مطابق نکته‌ی معادله‌ی آن به صورت$y=\frac {1}{2}x-1$ می‌باشد. حال با توجه به نکته‌ی راه حل اول، خط را تعیین علامت می‌کنیم.