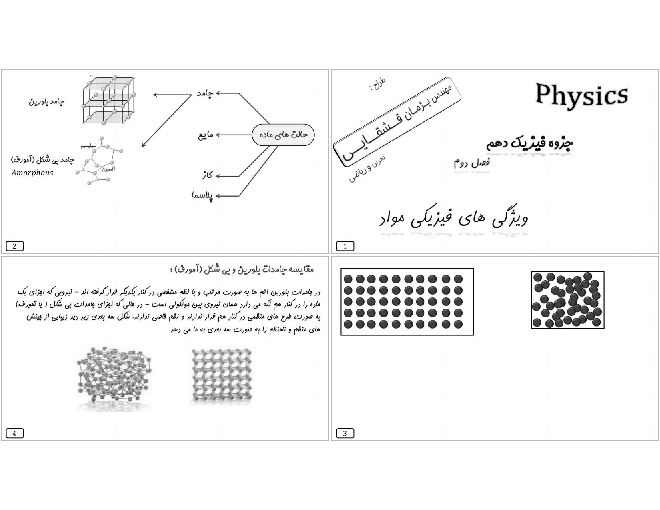
گام اول: قبل از تماس دو کره به یکدیگر قانون کولن را برای آن‌ها می‌نویسیم:

$F = k\frac{{\left| {{q_1}} \right|\left| {{q_2}} \right|}}{{{r^2}}} \Rightarrow 9 \times {10^{ - 1}} = 9 \times {10^9}\frac{{\left| {{q_1}} \right|\left| {{q_2}} \right|}}{{{{(0/6)}^2}}}$

$ \Rightarrow \left| {{q_1}} \right|\left| {{q_2}} \right| = 36 \times {10^{ - 12}}{C^2}$

گام دوم: پس از تماس دو کره به یکدیگر بار کره‌ها هم‌اندازه و همنام با یکدیگر می‌شود و اندازهٔ بار هر کره از رابطهٔ زیر به دست می‌آید:

${q'_1} = {q'_2} = \frac{{{q_1} + {q_2}}}{2}$

در این حالت، طبق رابطهٔ قانون کولن داریم:  $F' = k\frac{{\left| {{{q'}_1}} \right|\left| {{{q'}_2}} \right|}}{{{r^2}}}$

$ \Rightarrow 1/6 = 9 \times {10^9} \times \frac{{|\frac{{{q_1} + {q_2}}}{2}||\frac{{{q_1} + {q_2}}}{2}|}}{{{{(0/6)}^2}}}$

$ \Rightarrow {({q_1} + {q_2})^2} = 256 \times {10^{ - 12}} \Rightarrow |{q_1} + {q_2}| = 16 \times {10^{ - 6}}C$

گام سوم: با حل دو معادله و دو مجهول به دست آمده، ${q_1} =  + 2\mu C$ و ${q_2} =  - 18\mu C$ است.

تذکر: به جای دو معادله و دو مجهول به دست آمده، می‌توانستید از جای‌گذاری گزینه‌ها در این دو معادله استفاده کنید.