درس 2: مشتق‌پذیری و پیوستگی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
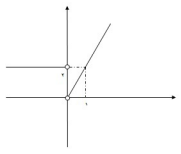
تابع $f(x) = \left\{ \begin{gathered}
{x^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x \geqslant 0 \hfill \\
2x + 1\,\,\,\,\,\,\,\,x \lt 0 \hfill \\
\end{gathered} \right.$ داده شده است؛
الف) نشان دهید که $f'(0)$ وجود ندارد.
ب) ضابطه تابع مشتق را بنویسید.
ج) نمودار تابع $f'$ را رسم کنید.
پاسخ تشریحی :
تحلیل ویدئویی تست
امیرحسین مزدور 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...