كدام گزاره همواره درست است؟
1 )
اگر $f$ در دامنهاش پيوسته باشد، آنگاه دارای اكسترمم مطلق است.
2 )
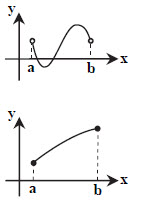
اگر $f$ بر بازهٔ $\left( a,b \right)$ پيوسته باشد، در اين بازه اكسترمم مطلق ندارد.
3 )
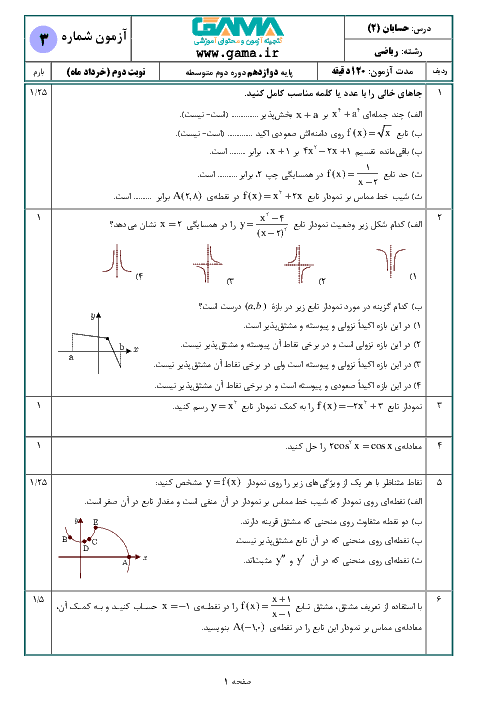
اگر $f$ بر بازهٔ $\left[ a,b \right]$ پيوسته باشد، در اين بازه دارای اكسترمم نسبی است.
اگر $f$ بر بازهٔ $\left( a,b \right)$ پيوسته و دارای اكسترمم مطلق باشد، آنگاه دارای اكسترمم نسبی است.
پاسخ تشریحی :