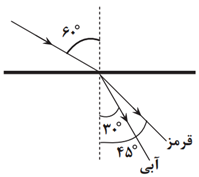
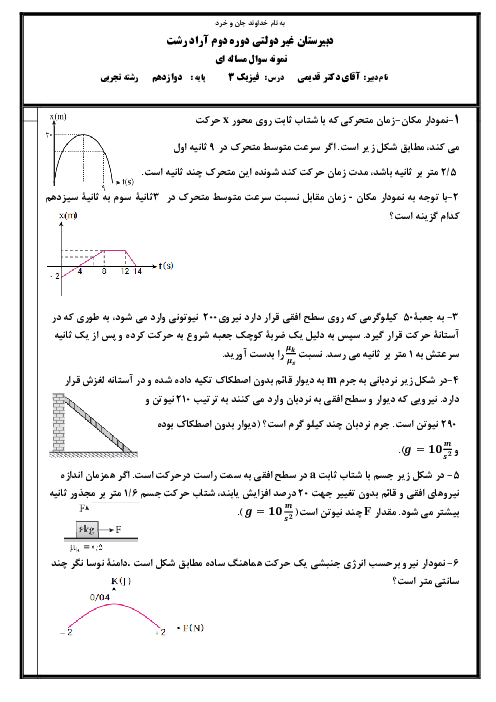
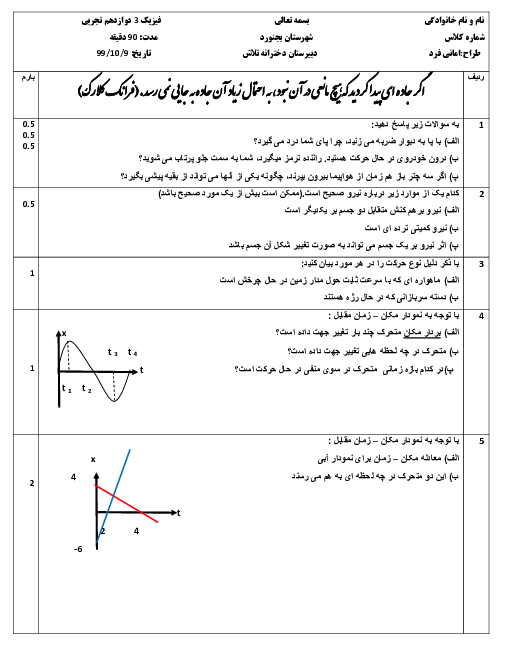
با رسم شكل و طبق رابطهٔ اسنل به محاسبهٔ زاويهٔ شكست برای پرتوی نور میپردازيم:
${{n}_{1}}\times \sin \hat{i}$ قرمز $=n$ قرمز $\times \sin \hat{r}$
$\xrightarrow[\hat{i}={{60}^{{}^\circ }},{{n}_{1}}=1]{n=\sqrt{\frac{3}{2}}}1\times \frac{\sqrt{3}}{2}=\sqrt{\frac{3}{2}}\times \sin \hat{r}$
$\Rightarrow \sin \hat{r}=\frac{\sqrt{2}}{2}\Rightarrow \hat{r}$ قرمز $={{45}^{{}^\circ }}(1)$
${{n}_{1}}\times \sin \hat{i}$ آبی $=n$ آبی $\times \sin \hat{r}$
$\xrightarrow[\hat{i}={{60}^{{}^\circ }},{{n}_{1}}=1]{n=\sqrt{3}}1\times \frac{\sqrt{3}}{2}=\sqrt{3}\times \sin {\hat{r}}'$
$\Rightarrow \sin {\hat{r}}'=\frac{1}{2}\Rightarrow {\hat{r}}'$ آبی $={{30}^{{}^\circ }}(2)$
$(1),(2)\Rightarrow \hat{r}$ آبی $-{\hat{r}}'$ قرمز $={{15}^{{}^\circ }}$