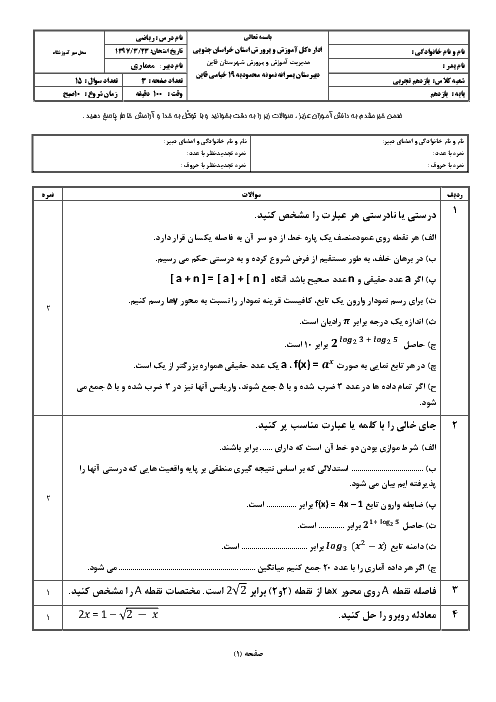
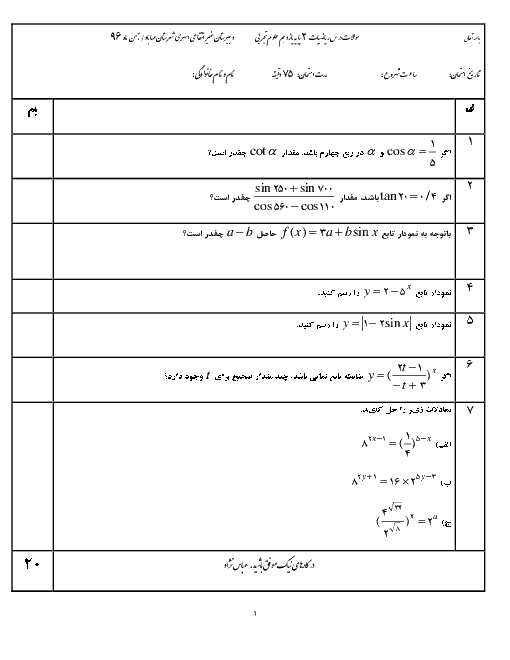
درس 3: معادلات گویا و معادلات رادیکالی
ریاضی (2)
یازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
اگر $x=2$ یکی از ریشه‌های معادلهٔ $\frac{a}{x+1}=\frac{a-2x}{{{x}^{3}}+1}+\frac{3a-1}{{{x}^{2}}-x+1}$ باشد، ریشهٔ دیگر این معادله کدام است؟
1 )
$x=-1$
2 )
$x=\frac{3}{4}$
3 )
$x=-\frac{1}{2}$
معادله ریشهٔ دیگری ندارد.
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...