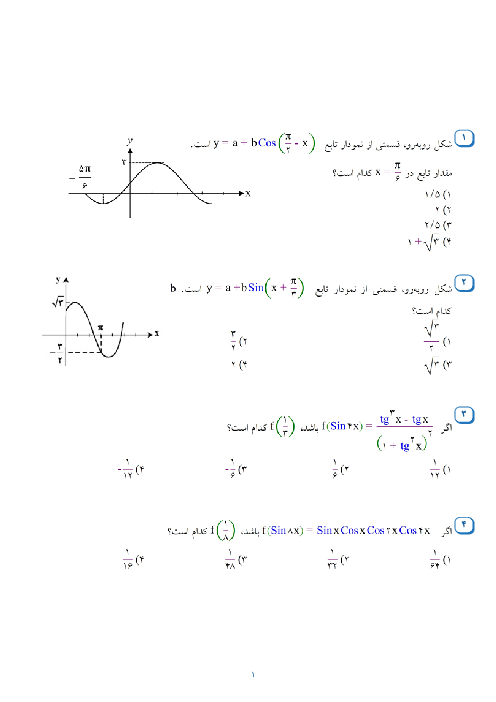
خط $d$ به معادله $y - x = 0$، عمودمنصف خطالمرکزین دو دایره است که شعاع یکی 2 برابر دیگری است. اگر خط $d$ بر دایره کوچک‌تر به معادله ${x^2} + {y^2} + 6x - 2y = r$ مماس باشد، حاصل‌ضرب طول نقاط برخورد دو دایره کدام است؟
$\frac{5}{2}$
2 )
$\frac{5}{4}$
3 )
$\frac{{65}}{{32}}$
4 )
$\frac{{65}}{{64}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مرتبط
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...