در شکل روبه‌رو توپی به جرم را در بالاترین نقطه‌ی مسیرش می‌بینید. در این نقطه نیروی خالص وارد بر جسم و نیروی مقاومت هوا افقی است، شتاب حاصل از نیروی مقاومت هوا… | فیزیک (3) ریاضی دوازدهم شماره 66731

موبایل / ایمیل

قوانین و مقررات را خواندم و می پذیرم.

لطفا کدی که به {{ identity }} ارسال شده است را وارد کنید.

کد فعال سازی :

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

لطفا برای حساب خود رمز عبور انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

انصراف

موبایل / ایمیل

ورود | ثبت نام

لطفا کدی که برای شما ارسال شده است را وارد کنید.

کد فعال سازی :

ارسال مجدد کد فعال سازی {{ countDown }}

منتظر دریافت پیامک شما ...

برای حساب خود رمز عبور جدید انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

انصراف

لطفا کمی صبر کنید ...

موبایل / ایمیل

رمزعبور

رمز عبور خود را فراموش کردید؟ بازیابی کنید.

هنوز عضو نشده اید؟ ثبت نام کنید.

انصراف

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

قسمت 2: معرفی برخی از نیروهای خاص فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

در شکل روبه‌رو توپی به جرم $1/2kg$ را در بالاترین نقطه‌ی مسیرش می‌بینید. در این نقطه نیروی خالص وارد بر جسم $13N$ و نیروی مقاومت هوا افقی است، شتاب حاصل از نیروی مقاومت هوا برحسب متر بر مجذور ثانیه کدام است؟

1 )

$-5\overrightarrow{i}$

2 )

$5\vec{i}$

3 )

$-4/16\overrightarrow{i}$

4 )

$4/16\vec{i}$

نمایش پاسخ

گام اول: نیروی وزن را محاسبه می‌کنیم: $W=mg=1/2\times 10=12N$

گام دوم: نیروی وزن قائم و نیروی مقاومت هوا افقی است؛ پس بر هم عمود هستند و داریم:

$F=\sqrt{{{W}^{2}}+{{f}^{2}}}\Rightarrow 13=\sqrt{{{12}^{2}}+{{f}^{2}}}\Rightarrow {{13}^{2}}={{12}^{2}}+{{f}^{2}}\Rightarrow 169=144+{{f}^{2}}=25\Rightarrow f=5N$

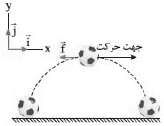
گام سوم: نیروی مقاومت هوا خلاف جهت حرکت است. پس مطابق شکل روبه‌رو، در بالاترین نقطه، این نیرو به طور افقی و به سمت چپ است. $\overrightarrow{f}=-5\overrightarrow{i}$

گام چهارم: پس شتاب حاصل از مقاومت هوا برابر است با: $\overrightarrow{a}=\frac{\overrightarrow{f}}{m}=\frac{-5\overrightarrow{i}}{1/2}\simeq (-4/16\overrightarrow{i}){m}/{{{s}^{2}}}\;$

گزارش خطا

پاسخ تشریحی :

تحلیل ویدئویی تست

با آلبوم تست

نمونه سوالات مرتبط