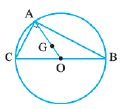
دایره‌ای بر مثلث $ABC$ که در رأس $A$ قائمیه است، محیط شده است. اگر نقاط $B$ و $C$ ثابت باشند و نقطهٔ $A$ روی محیط دایره حرکت کند، مکان هندسی نقطهٔ $G$ مرکز ثقل مثلث کدام است؟
دایره‌ای به شعاع $\frac{BC}{6}$
2 )
دایره‌ای به شعاع $\frac{BC}{4}$
3 )
دایره‌ای به شعاع $\frac{BC}{3}$
4 )
دایره‌ای به شعاع $\frac{BC}{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...