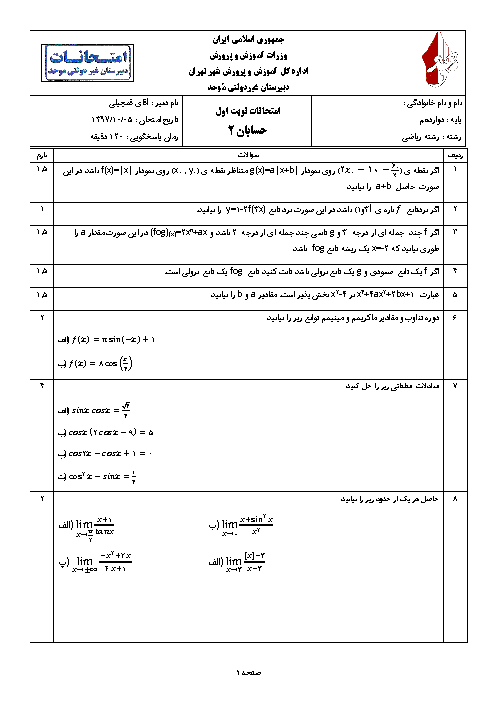
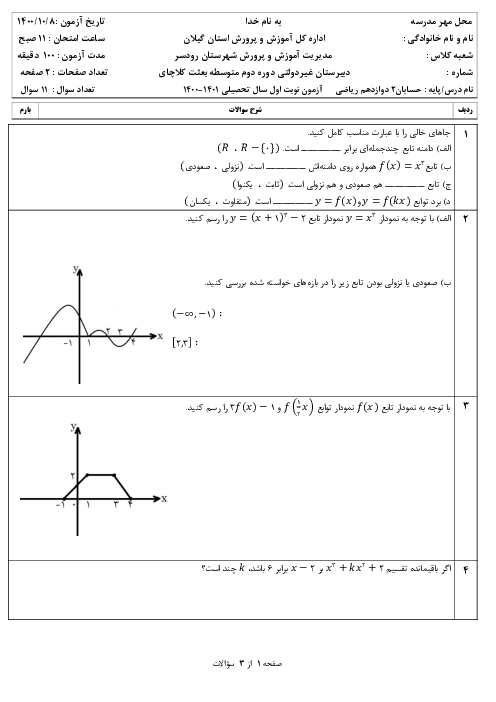
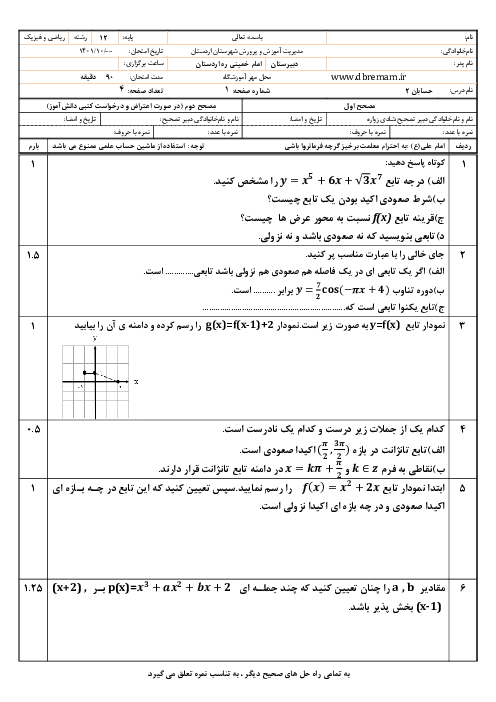
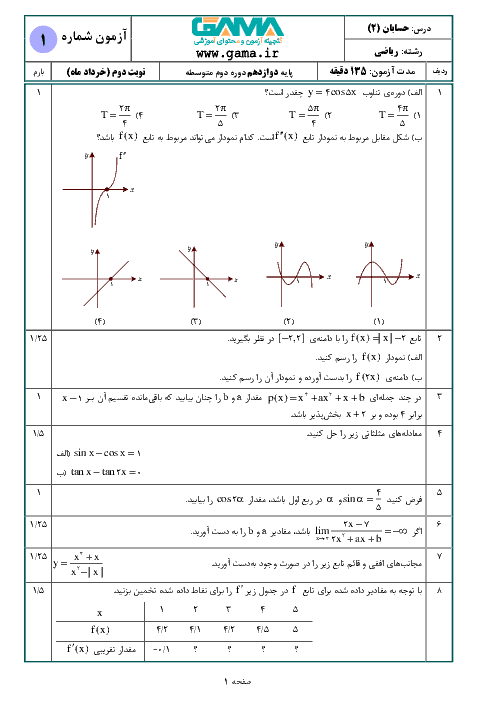
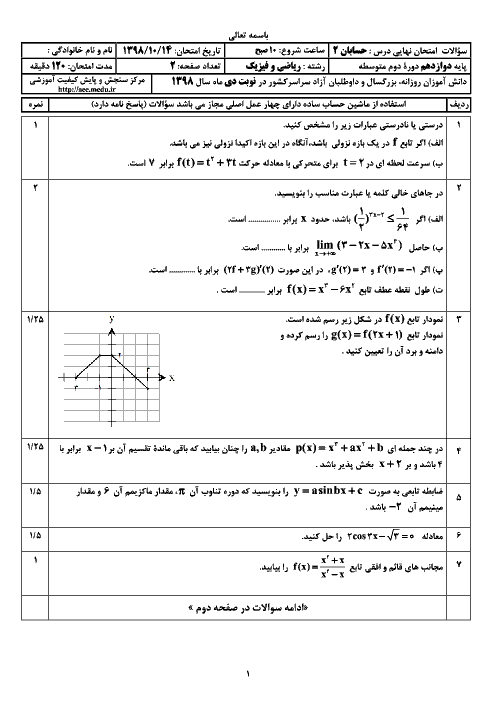
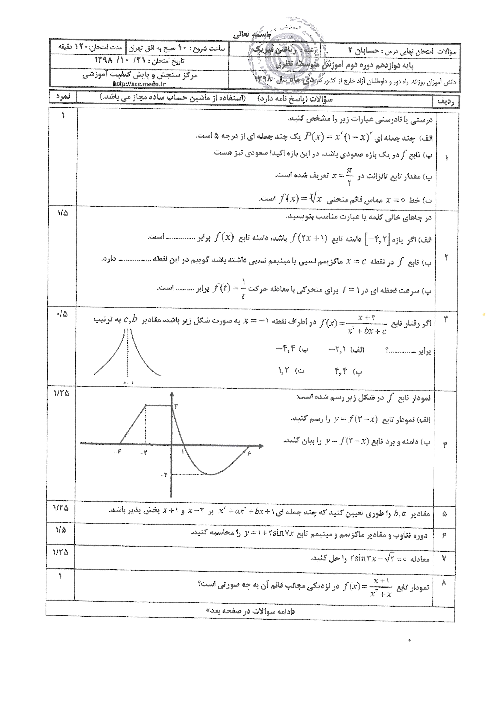
تابع $f$ در $x=0$ پیوسته است و حدهای چپ و راست تابع در این نقطه برابر با صفرند.

$\Rightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,f(x)=\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,f(x)=f(0)\Rightarrow \sqrt{2-\sqrt{4-{{({{0}^{+}})}^{2}}}}=\sqrt{2-\sqrt{4-{{({{0}^{-}})}^{2}}}}=0=f(0)$ 

${f}'(x)=\underset{x\to 0}{\mathop{\lim }}\,\frac{f(x)-f(0)}{x-0}=\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{2-\sqrt{4-{{({{0}^{-}})}^{2}}}}-0}{x}=\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{4-4+{{x}^{2}}}}{x(\sqrt{2+\sqrt{4-{{x}^{2}}}})}=\underset{x\to 0}{\mathop{\lim }}\,\frac{\left| x \right|}{2x}\Rightarrow \left\{ \begin{matrix}    {{{{f}'}}_{+}}(0)=\frac{1}{2}  \\    {{{{f}'}}_{-}}(0)=-\frac{1}{2}  \\ \end{matrix} \right.$ 

تابع $f(x)$ در $x=0$ مشتق چپ و مشتق راست نابرابر دارد، پسدر این نقطه مشتق‌پذیر نیست.