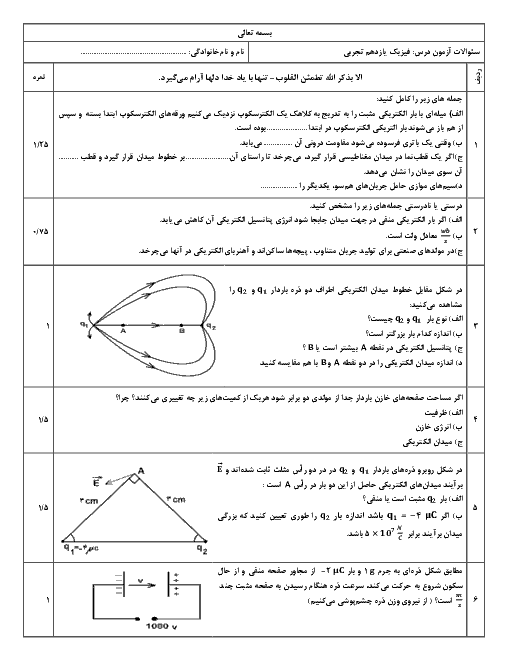
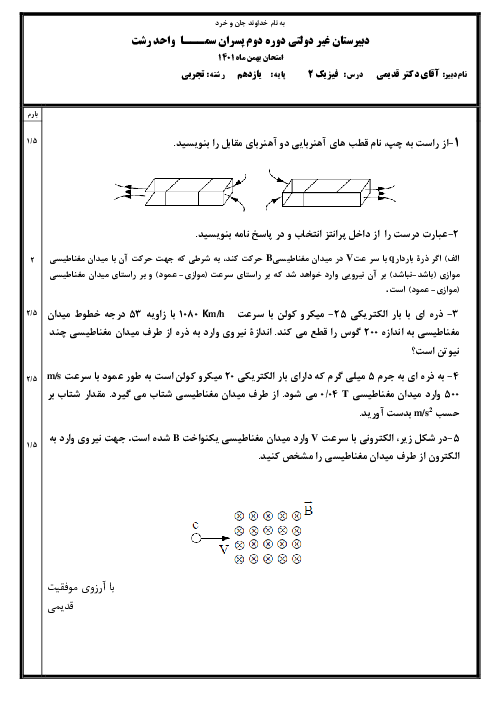
قدم اول: برای اینکه هر سه ذره در حال تعادل باشند، (باید برایند نیروهای وارد بر هر یک صفر باشد)، بار ${{q}_{3}}$ باید بین دو بار همنام ${{q}_{1}}$ و ${{q}_{2}}$ قرار گیرد و بدیهی است که نزدیکتر به بار با اندازهٔ کوچکتر یعنی ${{q}_{1}}$. حال در ابتدا مکان قرار گرفتن ${{q}_{3}}$ را مییابیم.
با توجه به تصویر 1
${{F}_{3}}=0\,\Rightarrow {{F}_{13}}={{F}_{23}}\,\Rightarrow \,\frac{k\left| {{q}_{1}} \right|\left| {{q}_{3}} \right|}{r_{13}^{2}}=\frac{k\left| {{q}_{2}} \right|\left| {{q}_{3}} \right|}{r_{23}^{2}}\,\xrightarrow[\left| {{q}_{2}} \right|=12\mu C]{\left| {{q}_{1}} \right|=3\mu C}\frac{3}{{{x}^{2}}}=\frac{13}{{{(15-x)}^{2}}}$
بعد از ساده کردن از طرفین جذر میگیریم.
$\frac{1}{x}=\frac{2}{15-x}\Rightarrow x=5cm$
قدم دوم: برای اینکه هر سه ذره در حال تعادل باشند، باید برایند نیروهای وارد بر بار ${{q}_{1}}$ یا ${{q}_{2}}$ نیز صفر باشد. تعادل بار ${{q}_{2}}$ را برسی میکنیم. بدیهی است که برای صفر شدن برایند نیروهای وارد بر بار ${{q}_{2}}$ باید دو نیروی هماندازهٔ غیر همسو از طرف بارهای ${{q}_{1}}$ و ${{q}_{3}}$ به آن وارد شود. چون ${{q}_{1}}>0$ است 0>${{q}_{3}}$ خواهد بود داریم:
${{F}_{12}}={{F}_{32}}\Rightarrow \frac{k\left| {{q}_{1}} \right|\left| {{q}_{2}} \right|}{r_{12}^{2}}=\frac{k\left| {{q}_{3}} \right|\left| {{q}_{2}} \right|}{r_{32}^{2}}\Rightarrow \frac{3}{{{15}^{2}}}=\frac{\left| {{q}_{3}} \right|}{{{10}^{2}}}$
$\Rightarrow \left| {{q}_{3}} \right|=\frac{4}{3}\mu C\xrightarrow{{{q}_{3}}\lt0}{{q}_{3}}=-\frac{4}{3}\mu C$
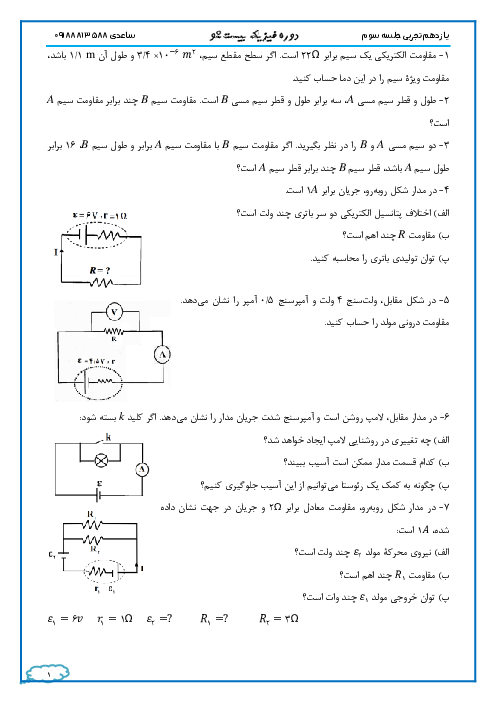
توجه به تصویر 2