درس 4: دنباله‌های حسابی و هندسی
ریاضی (1)
دهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
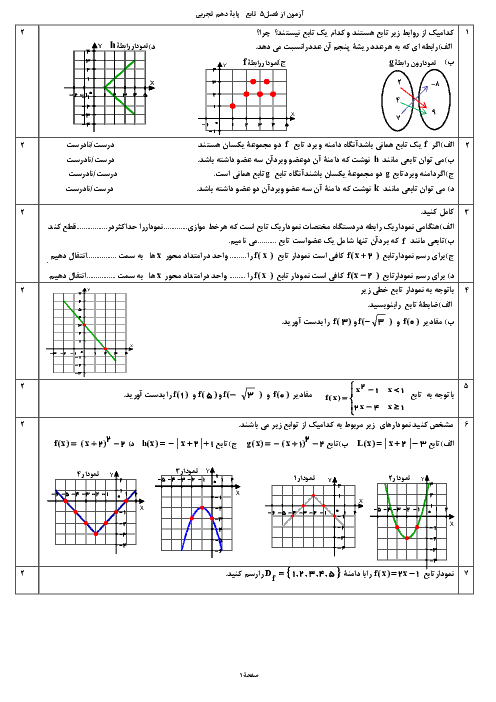
دو جمله اول یک دنباله هندسی ${{a}_{2}}=\frac{1}{\sqrt{3}-\sqrt{2}}$ و ${{a}_{1}}=\frac{1}{\sqrt{3}+\sqrt{2}}$ می‌باشد. مجموع سه جمله اول این دنباله کدام است؟
1 )
$\frac{5+2\sqrt{6}}{\sqrt{3}-\sqrt{2}}$
2 )
$\frac{5+2\sqrt{6}}{\sqrt{3}+\sqrt{2}}$
$11(\sqrt{3}+\sqrt{2})$
4 )
$\frac{11}{\sqrt{3}+\sqrt{2}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
ندا تقوی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...