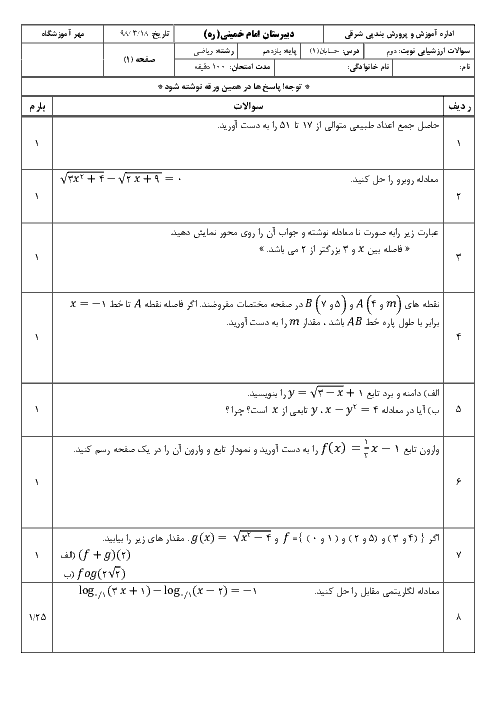
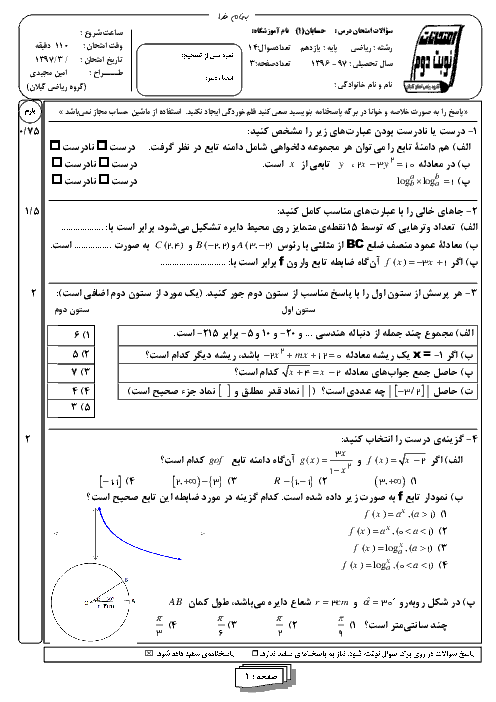
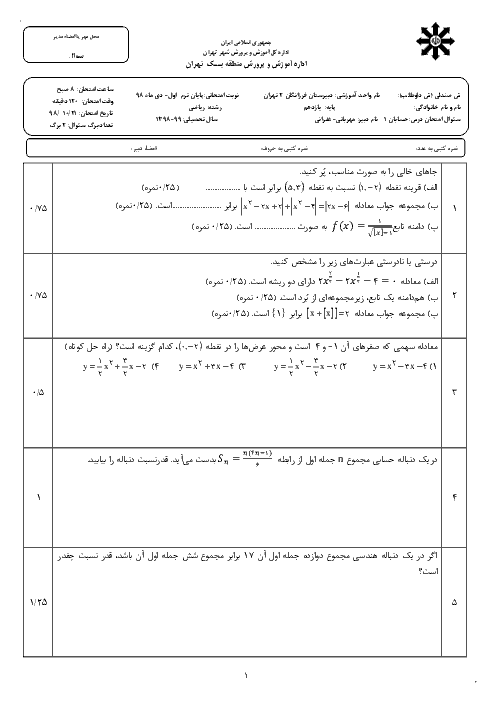
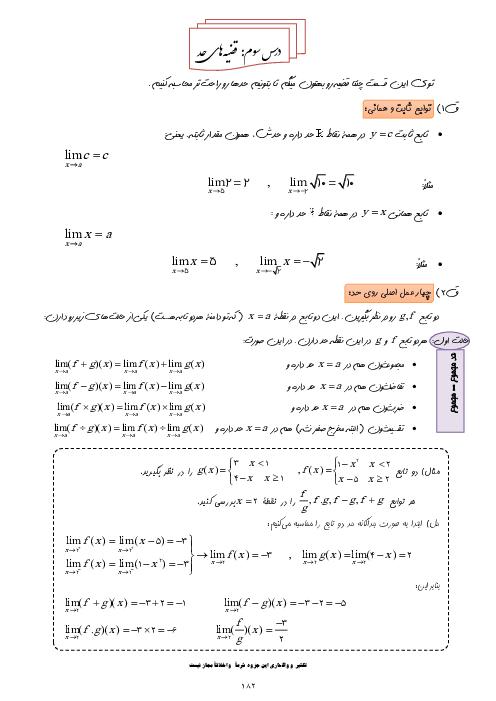
به ازای چه مقادیری از m معادلهٔ $m{x^2} - (4m - {m^3})x - m + 5 = 0$ دو ریشه دارد که قرینه یکدیگرند.
پاسخ تشریحی :
دو ریشه قرینه یکدیگرند. بنابراین مجموع ریشهها برابر صفر میشود. بنابر رابطه مجموع ریشهها داریم:
$s = 0 \to s = \frac{{ - b}}{a} = - \frac{{ - (4m - {m^3})}}{m} = 0\frac{{m(4 - {m^2})}}{m} = 0$
میدانیم کسری صفر است که صورتش صفر باشد. بنابراین:
$ \to (4m - {m^3}) = 0 \to m(4 - {m^2}) = 0 \to m = 0,4 - {m^2} = 0 \to {m^2} = 4 \to m = 2,m = - 2$
دو ریشه قرینه یکدیگرند. بنابراین حاصل ضرب ریشهها منفی است. با توجه رابطه حاصل ضرب ریشه داریم:
$p = \frac{c}{a} = \frac{{ - m + 5}}{m} < 0$
برای حل نامعادله کسری از جدول تعیین علامت استفاده میکنیم. ابتدا ریشه صورت و مخرج را به دست میآوریم. برای رسم جدول به صورت سریع علامت بزرگترین جمله صورت را در علامت بزرگترین جمله مخرج ضرب میکنیم. علامت به دست آمده را در جدول از سمت راست قرار میدهیم و سپس علامتها را یکی در میان عوض میکنیم. (شکل)
بنابراین جواب نامعادله با توجه به جدول $m < 0,m > 5$ قابل قبول است و در بین جوابهایی که برای m به دست آمد فقط $m = - 2$ قابل قبول است.

تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!