درس 2: استدلال ریاضی
ریاضی و آمار (2)
یازدهم
دوره دوم متوسطه- نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
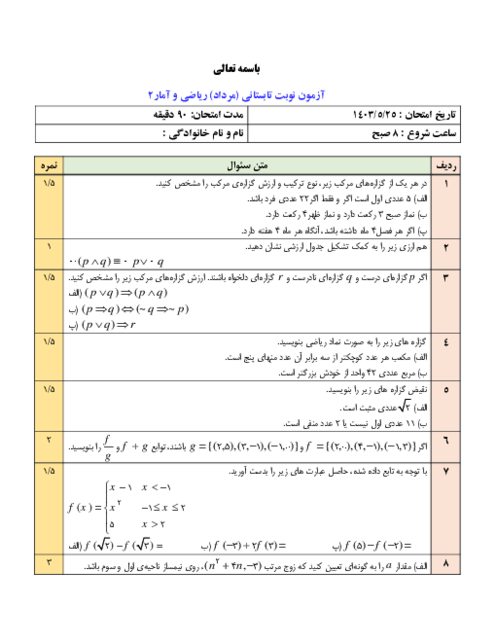
در مثال زیر خطا در گام چندم استدلال زیر باعث شده تا استدلالی غلط به‌دست آید؟
مثال: اگر $\sqrt[3]{\frac{{{(x+1)}^{2}}}{4}}\gt \sqrt[3]{\frac{{{(y+1)}^{2}}}{4}}$ آنگاه $x\gt y$
گام اول: $\sqrt[3]{\frac{{{(x+1)}^{2}}}{4}}\gt \sqrt[3]{\frac{{{(y+1)}^{2}}}{4}}$
گام دوم: ${{(\sqrt[3]{\frac{{{(x+1)}^{2}}}{4}})}^{3}}\gt {{(\sqrt[3]{\frac{{{(y+1)}^{2}}}{4}})}^{3}}$ طرفین را به توان 3 می‌رسانیم
گام سوم: $\frac{{{(x+1)}^{2}}}{4}\gt \frac{{{(y+1)}^{2}}}{4}$ رادیکال از طرفین حذف می‌شود
گام چهارم: $\sqrt{\frac{{{(x+1)}^{2}}}{4}}\gt \sqrt{\frac{{{(y+1)}^{2}}}{4}}$ از طرفین جذر می‌گیریم
گام پنجم: $\frac{x+1}{2}\gt \frac{y+1}{2}$ طرفین را در 2 ضرب می‌کنیم
گام ششم: $x+1\gt y+1$ 1 را از طرفین خذف می‌کنیم
گام هفتم: $x\gt y$
1 )
دوم
2 )
سوم
3 )
چهارم
پنجم
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...