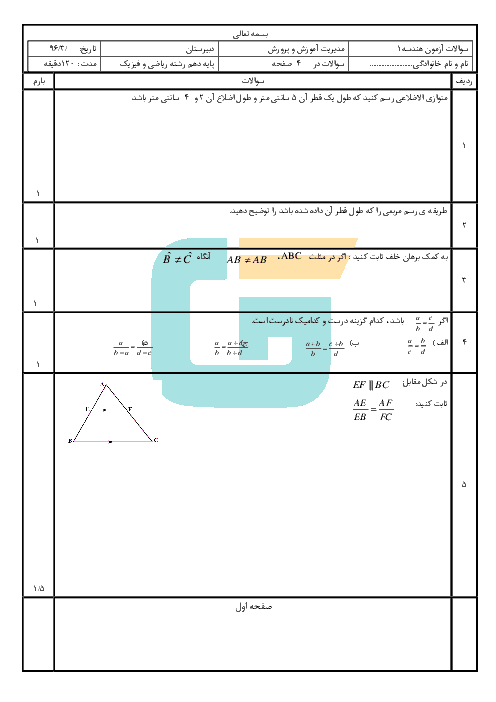فصل 2: قضیۀ تالس، تشابه و کاربردهای آن
هندسه (1)
دهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
در دو مثلث قائم الزاویه متشابه، اگر $a$ و ${a}'$ دو وتر مثلث و اضلاع $b$ و ${b}'$ و اضلاع $c$ و ${c}'$ با هم متناظر باشند، کدام رابطه همواره درست است؟
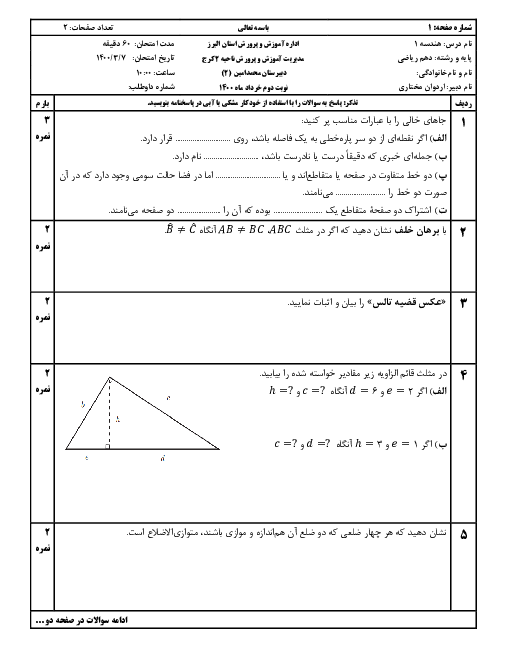
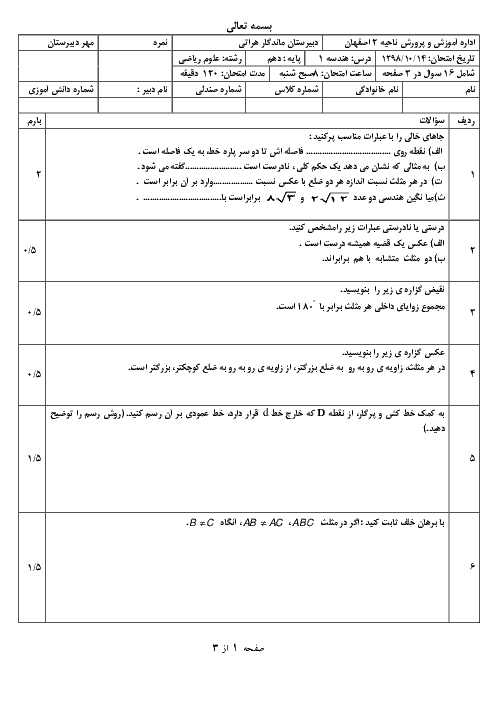
$a{a}'=b{b}'+c{c}'$
2 )
${{a}^{2}}+{{{a}'}^{2}}=b{b}'+c{c}'$
3 )
$c{c}'=\frac{a{a}'}{b{b}'}$
4 )
$\frac{a}{{{{{a}'}}^{2}}}=\frac{{b}'+{c}'}{{{b}^{2}}+{{c}^{2}}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...