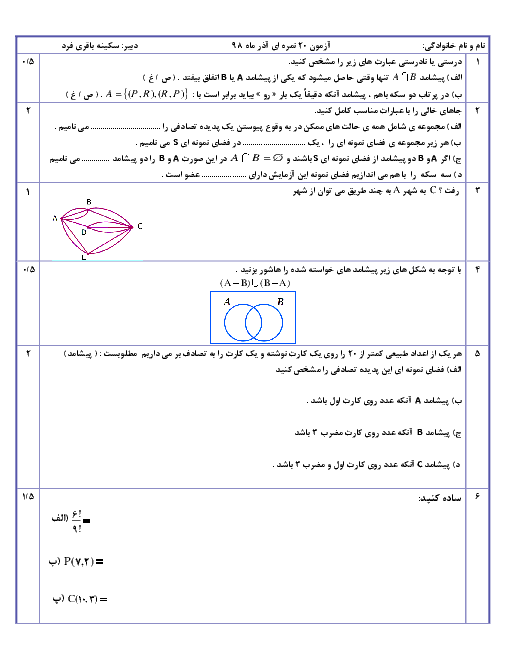
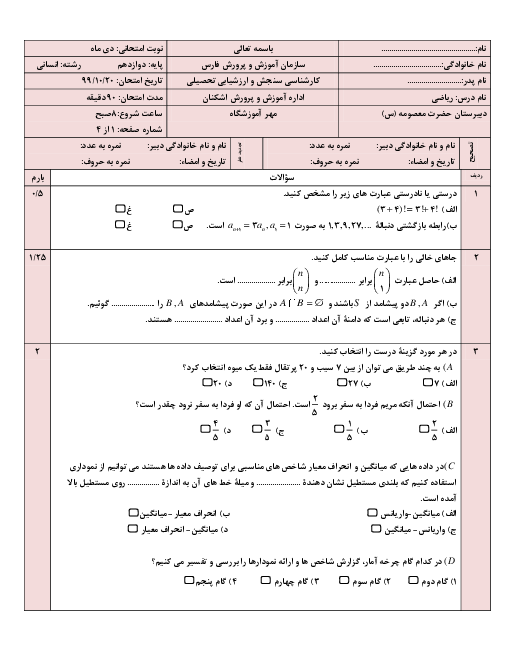
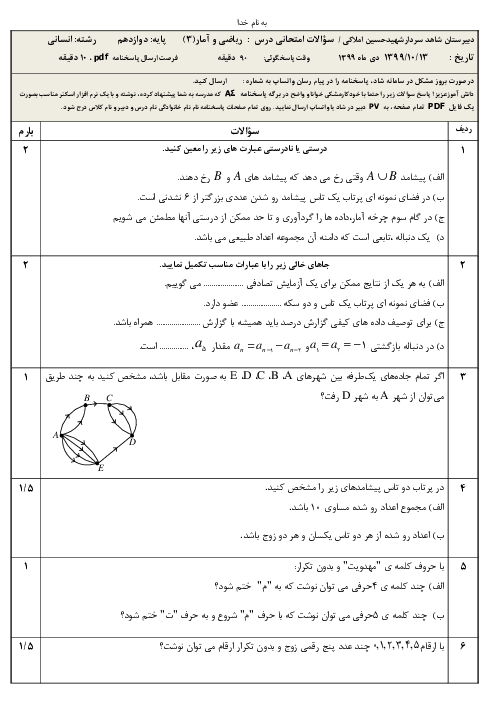
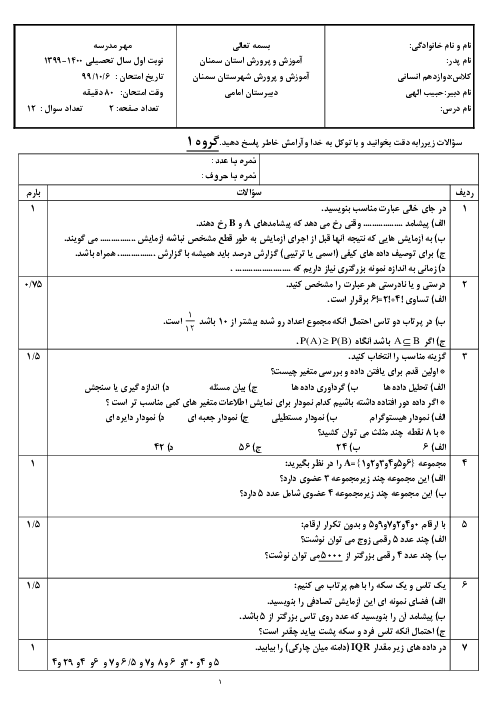
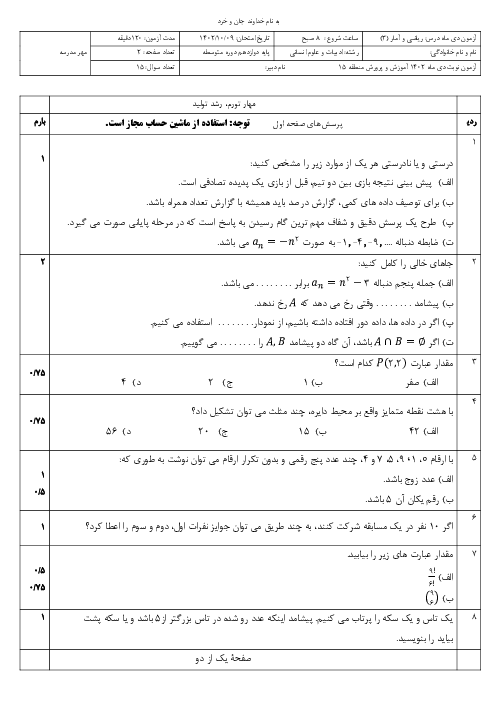
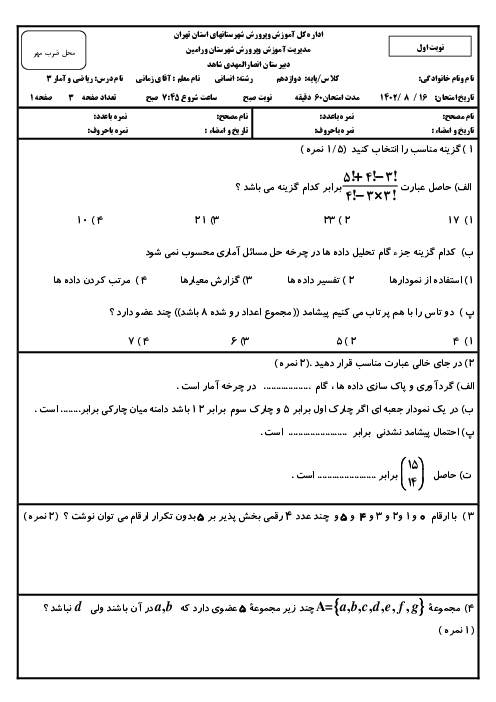
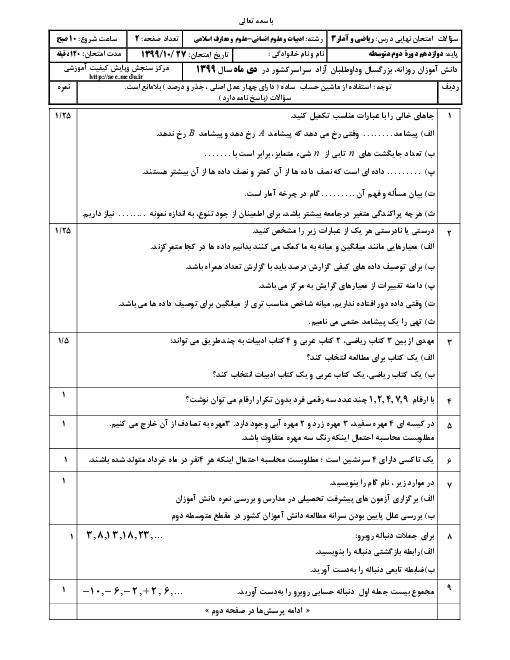
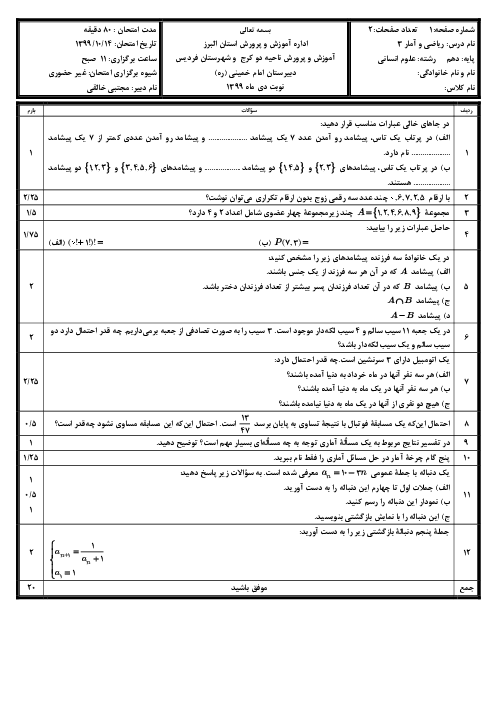
نکته: اگر ${{s}_{n}}$ مجموع $n$ جملۀ اول يك دنبالۀ هندسی يا حسابی باشد، داريم:

${{s}_{1}}={{a}_{1}}$ 

${{s}_{2}}={{a}_{1}}+{{a}_{2}}$ 

${{s}_{3}}={{a}_{1}}+{{a}_{2}}+{{a}_{3}}$ 

${{s}_{n}}={{a}_{1}}+{{a}_{2}}+...{{a}_{n}}$

ابتدا با توجه به نکته می‌توان نوشت:

$\left\{ \begin{matrix}    \begin{matrix}    {{a}_{1}}=10  \\      {{a}_{2}}=10\times \frac{1}{3}  \\    {{a}_{3}}=10\times {{\left( \frac{1}{3} \right)}^{2}}  \\    \begin{align}   & {{a}_{4}}=10\times {{\left( \frac{1}{3} \right)}^{3}}\Rightarrow {{s}_{n+1}}=10+10\times \left( \frac{1}{3} \right)+10\times {{\left( \frac{1}{3} \right)}^{2}}+10\times {{\left( \frac{1}{3} \right)}^{3}}+...+10\times {{\left( \frac{1}{3} \right)}^{n}} \\  & {{a}_{n}}=10\times {{\left( \frac{1}{3} \right)}^{n-1}}\Rightarrow {{s}_{n+1}}=10+\frac{1}{3}\left( \underbrace{10+10\times \left( \frac{1}{3} \right)+10\times {{\left( \frac{1}{3} \right)}^{2}}+...+10\times {{\left( \frac{1}{3} \right)}^{n-1}}}_{{{s}_{n}}} \right)\Rightarrow {{s}_{n+1}}=10+\frac{1}{3}{{s}_{n}} \\  & {{a}_{n+1}}=10\times {{\left( \frac{1}{3} \right)}^{n}} \\ \end{align}  \\ \end{matrix}  \\ \end{matrix} \right.$

بنابراين رابطۀ بازگشتی مربوط به مجموع جملات اين دنباله به صورت زير است:

$\left\{ \begin{matrix}    {{s}_{n+1}}=10+\frac{1}{3}{{s}_{n}}  \\    {{s}_{1}}=10  \\ \end{matrix} \right.$ 

تذكر: در حالت كلي رابطۀ بازگشتی يك دنبالۀ هندسی با جملۀ اول ${{a}_{1}}$ و نسبت مشترک $r$ صورت زیر است:

${{a}_{n+1}}=r{{a}_{n}},{{a}_{1}}=a$ 

كه از اين رابطه برای به دست آوردن رابطۀ بازگشتی مربوط به مجموع جملات يك دنبالۀ هندسی نيز می‌توان استفاده كرد.