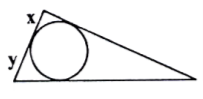
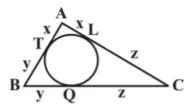
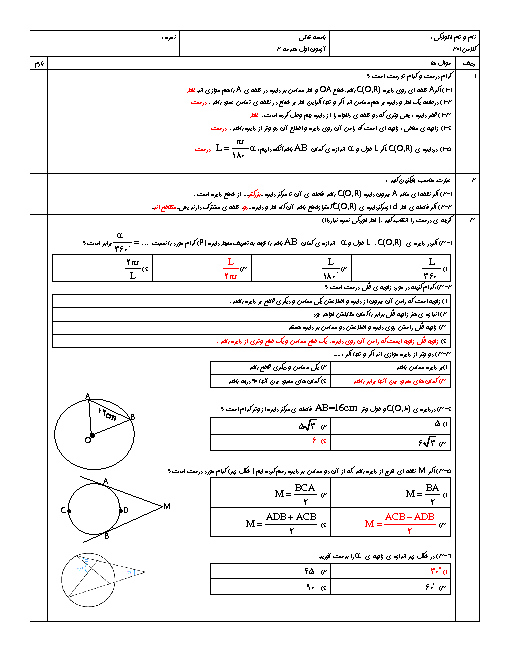
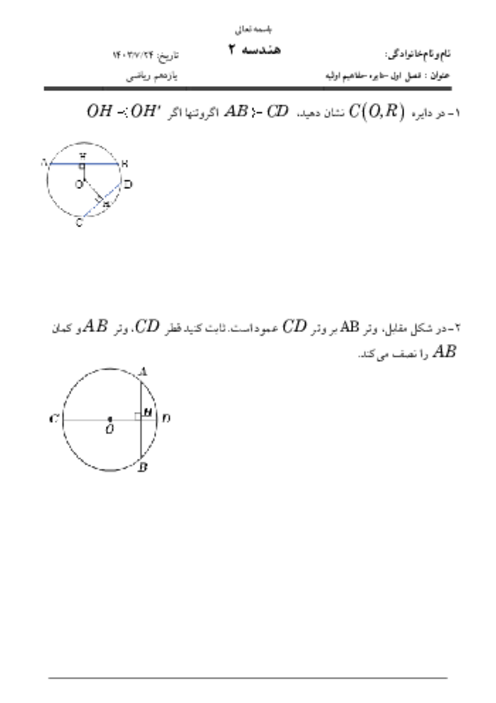
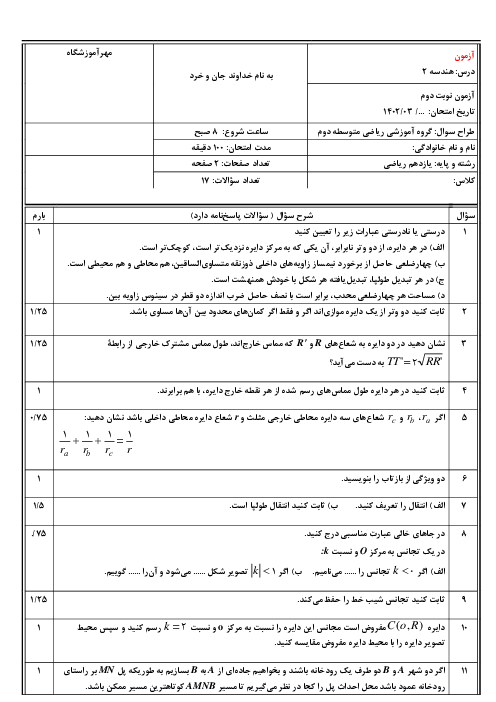
درس 3: چند ضلعیهای محاطی و محیطی
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
دایرهٔ محاطی داخلی یک مثلث به طول اضلاع $13$، $9$ و $8$، در نقطهٔ تماس، کوچکترین ضلع را به دو قطعه تقسیم میکند. نسبت آن دو قطعه کدام است؟