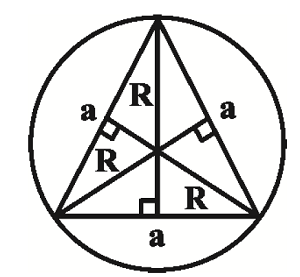
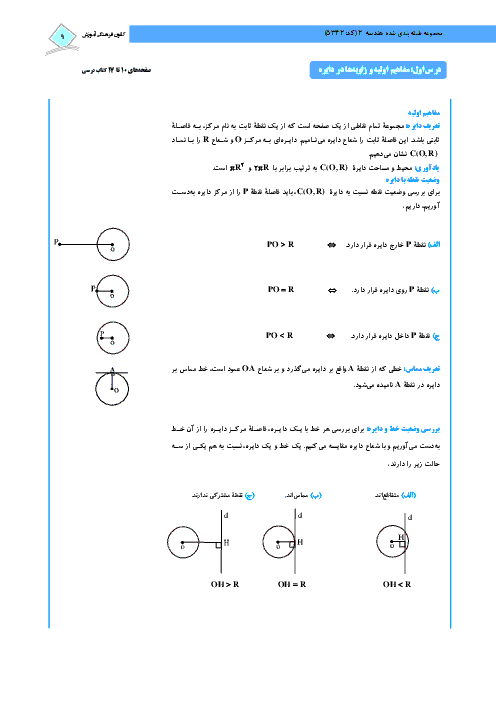
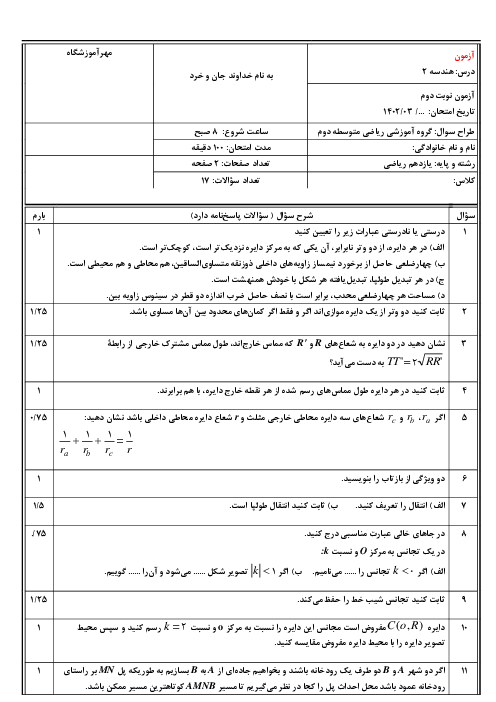
ضلع مثلث متساویالاضلاع را a درنظر میگیریم.
حال باتوجه به تصویر و ویژگیهای این مثلث داریم:
$\begin{align} & R=\frac{2}{3}(\frac{a\sqrt{3}}{2})\Rightarrow R=\frac{a\sqrt{3}}{3} \\ & r=\frac{S}{P}=\frac{\frac{{{a}^{2}}\sqrt{3}}{4}}{\frac{3a}{2}}\Rightarrow r=\frac{a\sqrt{3}}{6} \\ & {{r}_{a}}=\frac{S}{P-a}=\frac{\frac{{{a}^{2}}\sqrt{3}}{4}}{\frac{3a}{2}-a}=\frac{\frac{{{a}^{2}}\sqrt{3}}{4}}{\frac{a}{2}}\Rightarrow {{r}_{a}}=\frac{a\sqrt{3}}{2} \\ & r+R=\frac{a\sqrt{3}}{6}+\frac{a\sqrt{3}}{3}=\frac{a\sqrt{3}}{6}+\frac{2a\sqrt{3}}{6}=\frac{a\sqrt{3}}{2}\Rightarrow r+R={{r}_{a}} \\ \end{align}$