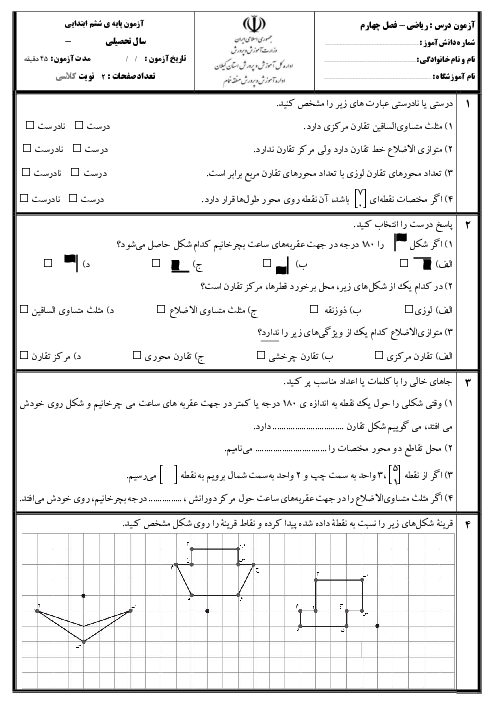
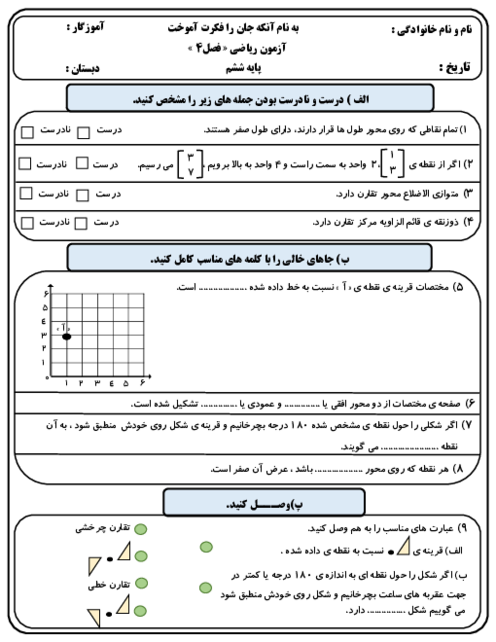
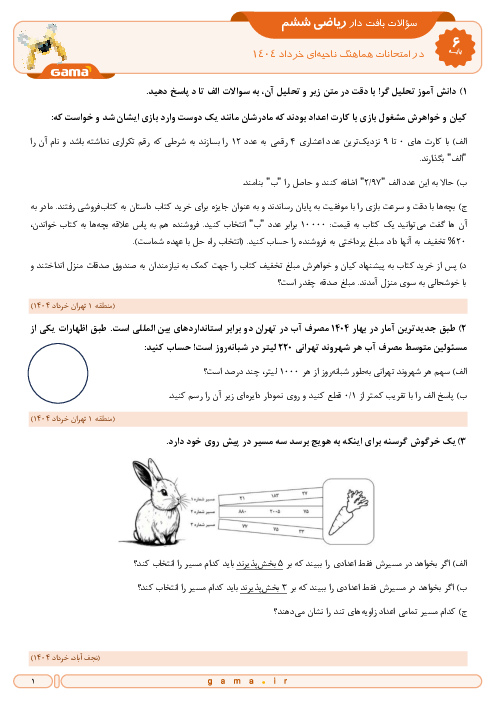
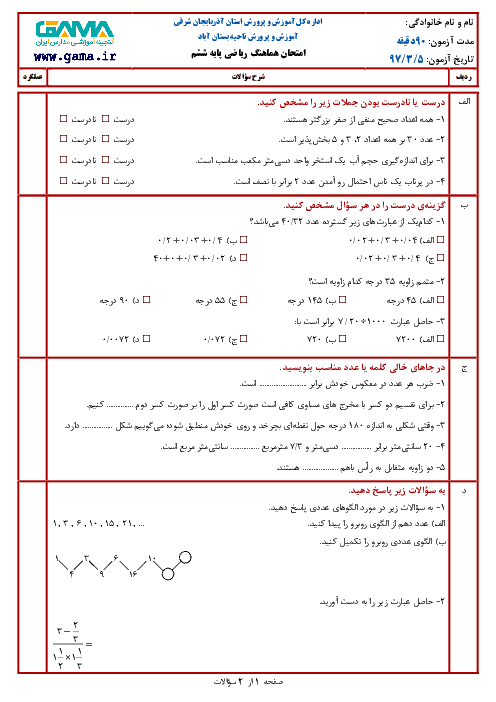
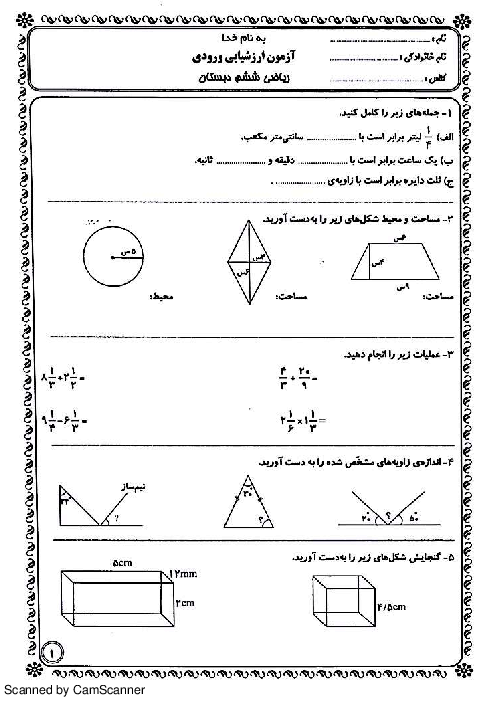
اگر مختصات رأس‌های مستطیلی $\left[ \begin{matrix} 0 \\2\\ \end{matrix} \right]$، $\left[ \begin{matrix} 3 \\2\\ \end{matrix} \right]$، $\left[ \begin{matrix} 3 \\0\\ \end{matrix} \right]$ و $\left[ \begin{matrix} 0 \\0\\ \end{matrix} \right]$ باشند با ضرب کردن مختصات رأس‌های آن در 3 (یعنی ضرب کردن مؤلفه‌های افقی و عمودی در 3) مستطیل جدیدی به دست می‌آید، مساحت آن چه عددی است؟
تحلیل ویدئویی تست
ریحانه احمدی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...