مقادیر و و را در تابع طوری به دست آورید که در شرایط زیر صدق کند. و و طول نقطه عطف نمودار تابع باشد.

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

ریاضی پنجم فصل اول ریاضی ششم فصل اول الگوی مثلثی عدد شش رقمی بدون تکرار تغییر فیزیکی و شیمیایی ریاضی چهارم خط به خط زیست دهم جمله خبری نهاد چیست چه اعدادی بر ۶ بخش پذیرند مسند چیست مراحل روش علمی درس اول زبان هشتم با معنی و تلفظ

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

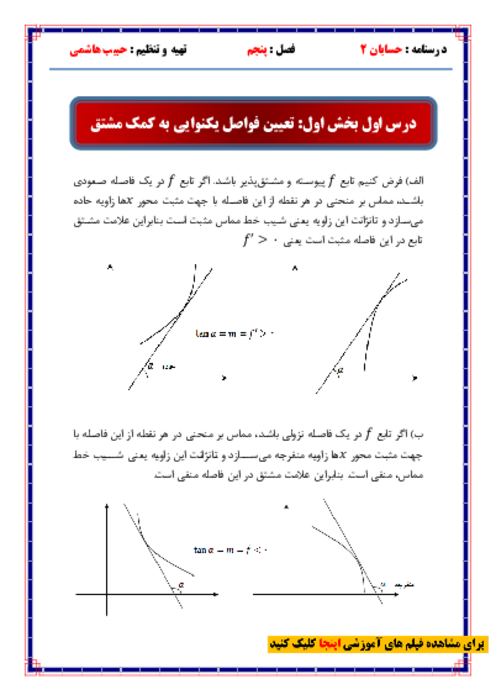
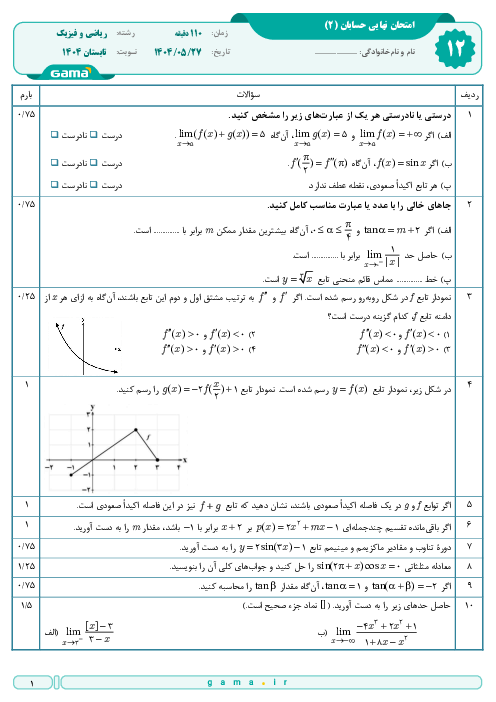
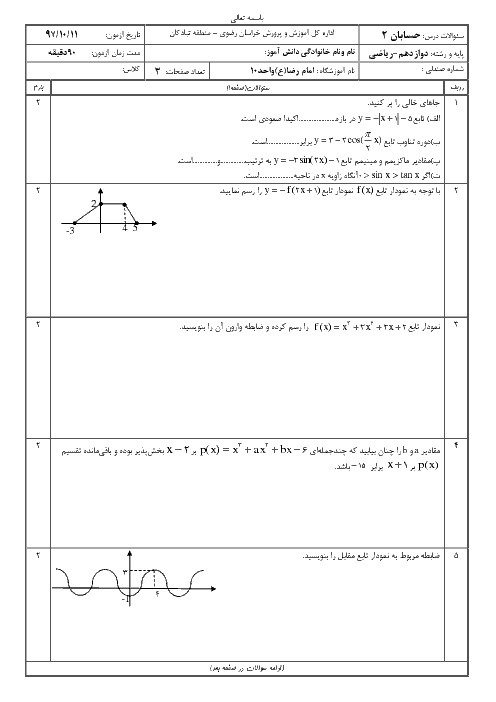
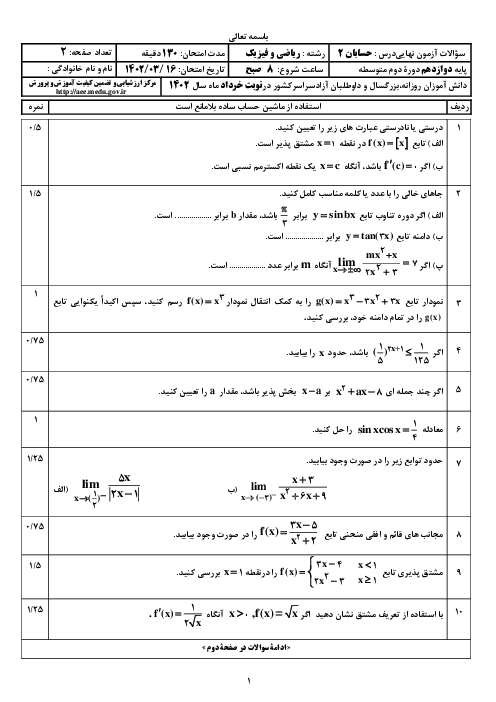
درس 2: جهت تقعر نمودار یک تابع و نقطۀ عطف آن حسابان (2) دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

مقادیر $a$ و $b$ و $c$ را در تابع $f(x) = a{x^3} + b{x^2} + c$ طوری به دست آورید که در شرایط زیر صدق کند.
$f(0) = 1$ و $f(1) = 2$ و $x = \frac{1}{2}$ طول نقطه عطف نمودار تابع $f$ باشد.

نمایش پاسخ

$f(0) = 1 \Rightarrow c = 1 $

$\Rightarrow f(x) = a{x^{\text{3}}} + b{x^2} + 1$

$\begin{array}{*{20}{c}}
{f(1) = 2 \Rightarrow a + b + 1 = 2 \Rightarrow a + b = 1} \\
{f''\left( {\frac{1}{2}} \right) = 0 \Rightarrow 3a + 2b = 0}
\end{array}$

$ \Rightarrow \begin{array}{*{20}{c}}
{a = - 2} \\
{b = 3}
\end{array}$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده