درس 1: اکسترمم‌های یک تابع و توابع صعودی و نزولی
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
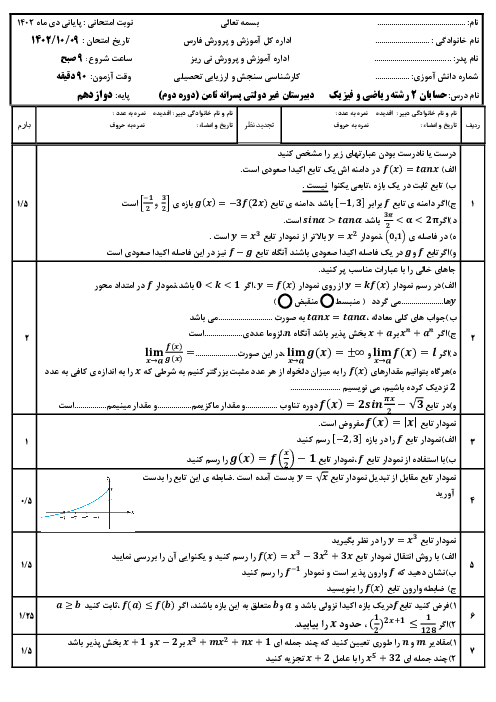
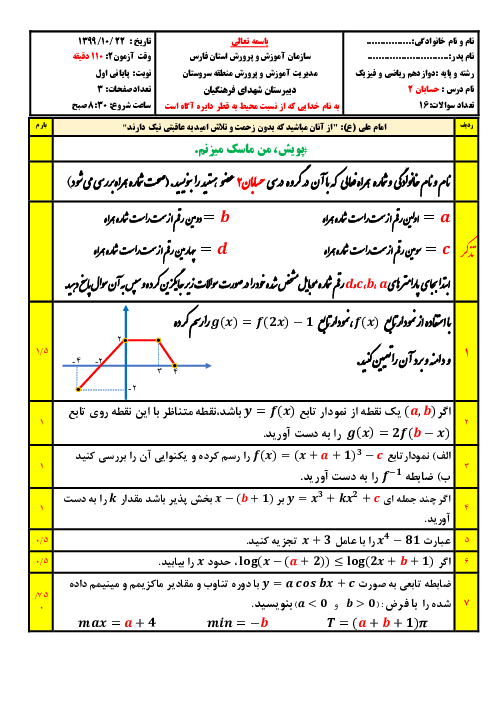
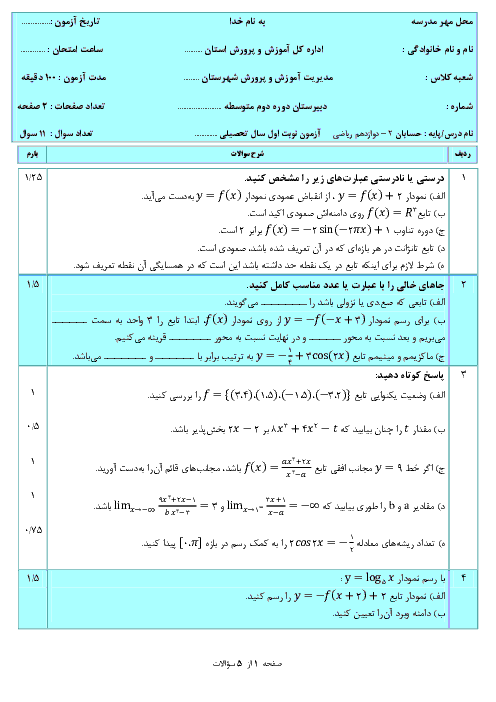
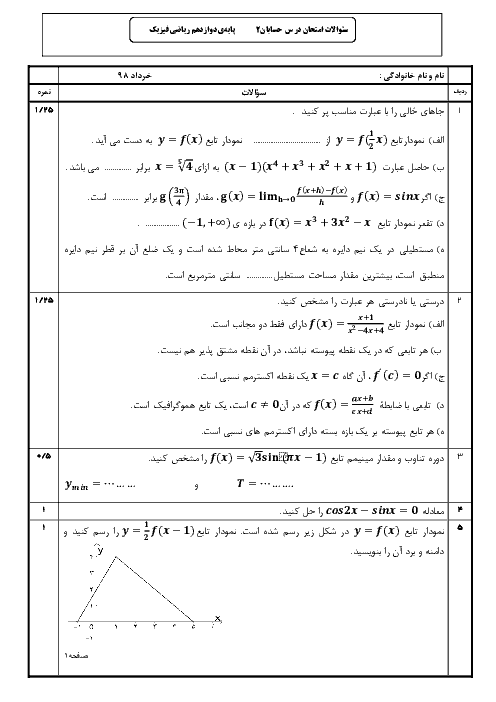
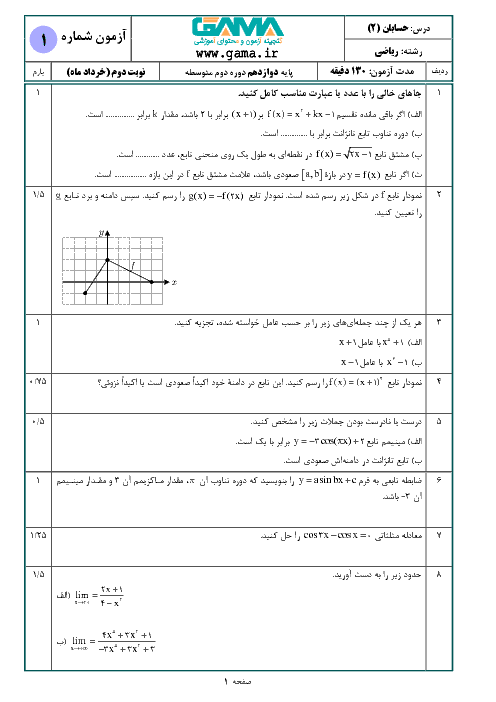
تابع با ضابطهٔ $f(x)=\left| {{x}^{2}}-1 \right|$ بر بازهٔ $\left[ -2,2 \right]$ ............
1 )
مشتقپذير است و می‌نیمم مطلق دارد.
2 )
مشتقپذير است و می‌نیمم مطلق ندارد.
مشتقپذير نیست ولی ماکزیمم مطلق دارد.
4 )
مشتقپذير نیست و می‌نیمم مطلق ندارد.
پاسخ تشریحی :
تحلیل ویدئویی تست
امیرحسین مزدور 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...