درس 4: قضیۀ هرون (محاسبۀ ارتفاعها و مساحت مثلث)
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
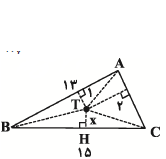
در مثلثی به اضلاع 4، 13 و 15 سانتیمتر، نقطهای درون مثلث از اضلاع به طول 4 و 13، به ترتیب به فاصلهٔ 2 و 1 سانتیمتر است. این نقطه از ضلع بزرگتر مثلث چه فاصلهای بر حسب سانتیمتر دارد؟